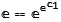2

Sometimes, DSolve would return

Inverse functions are being used by Solve, so some solutions may not be found

but it seems it has returned all results. For example,

DSolve[{y'[x]*Sin[x] == y[x]*Log[y[x]], y[Pi/2] == E}, y[x], x]

produces

{{y[x] -> E^Tan[x/2]}}

I calculated by myself, it seems this is the expression of all results. So, is there other results or bug?

Y. zeng
  • 567
  • 2
  • 6
  • 1
    As the warning says, "some solutions may not be found". – xzczd Dec 04 '23 at 08:17
  • @xzczd It's not sure whether it's found all the solutions even if it has found all? – Y. zeng Dec 04 '23 at 08:19
  • Yes, that's it. – xzczd Dec 04 '23 at 08:24
  • @xzczd Thanks. Is there a way to tell if mathmatica has found all the solutions, except calculating by ourselves? – Y. zeng Dec 04 '23 at 08:26
  • 1
    If what you want is a general method, I'm afraid the answer is no. Just search the warning message in this site, you'll see quite a number of discussion e.g. this one: https://mathematica.stackexchange.com/q/148226/1871 – xzczd Dec 04 '23 at 08:31
  • @RolandF And then what will happen? – Y. zeng Dec 04 '23 at 12:20
  • 1
    Do you see the Ulrich Neumann's answer who said that so many blue line are also the solution for that equation? Answering your comment for one of the answers below: These blue lines are the family of solutions. But once you fix the initial conditions, only one member becomes the only solution. All others go away. – Nasser Dec 04 '23 at 14:48
  • @Nasser Yes. I now know what the figure means. – Y. zeng Dec 04 '23 at 14:51

3 Answers3

2

Perhaps somewhat more descriptive than the mathematical answer @RolandF:

Show[{StreamPlot[{1, y *Log[y ]/Sin[x]}, {x, 0, Pi}, {y, 0, 2 E}], 
Plot[Exp[Tan[x/2]], {x, 0, 10}, PlotStyle -> Black], 
Graphics[{PointSize[Large], Point[{Pi/2, E}]}]}]

enter image description here

Ulrich Neumann
  • 53,729
  • 2
  • 23
  • 55
2

To add to all the good answers, we can try to find out why DSolve generated this message by solving the ode step by step. First generate the solution solution with no IC, then solve the constant of integration manually. This shows why Mathematica gave such message.

It is because without assuming the domain is real, the solution of the constant of integration is not unique. Only when adding assumption of Reals does it give same solution as DSolve gave directly

ClearAll["Global`*"];
ode=y'[x]*Sin[x]==y[x]*Log[y[x]];
ic = y[Pi/2] == E
directSolution = DSolve[{ode, ic}, y[x], x]

Mathematica graphics

Now lets do it step by step

sol = DSolve[ode, y[x], x][[1, 1]]

Mathematica graphics

Now setup the equation to solve for the constant of integration using given initial conditions

eq = sol /. {y[x] -> E, x -> Pi/2} /. Rule -> Equal

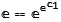
Mathematica graphics

Solve for c

 cSolution = Solve[eq, C[1]]

Mathematica graphics

Now if we use the above constant of integration and plug it back into the general solution we obtain

 sol /. cSolution // Simplify

Mathematica graphics

You see, for different $c_2,c_3$ there are different constant of integration $c_1$. But that all goes away if we solve in reals domain since then $c_2=0,c_3=0$ and what remains is $c_1=\ln 1$ which is zero.

if we now solve for $c_1$ using reals domain, now the same solution is obtained as above with DSolve with that extra message about some solutions might not be found:

 cSolution=Solve[eq,C[1],Reals]

Mathematica graphics

 sol /. cSolution // Simplify

Mathematica graphics

Mathematica internally works by default in complex domain. There is no way to pass assumptions to DSolve as far as I know. Basically the solution is unique if domain is real. I think what DSolve does, is at the end it must simplified the constant of integration to be real, but remembered that the solution had other complex values. So it returned back the solution assuming real, but issued that message because of this.

We have no access to the DSolve source code to check, but I think this is what happened.

Nasser
  • 143,286
  • 11
  • 154
  • 359
1

A first order differential equation has a unique solution passing through a point $ (x_0, y_0=y(x_0))$ in any open interval, running from boundary to boundary, if the right side of

$$y' = F(x,y) $$

satifies the Lipshitz condition

$$F(x,y+h) = F(x,y) + h g(x,y) + o(h^2 )$$ with $g(x,y)\ne 0$ everywhere. Since the solution starts with $(\pi/2, E)$ the Lipshitz condition is satisfied by $$F=y \log y /\sin x.$$ There are no other solutions of the integated equation$$\log \log y = \log\tan x/2 +c$$ passing the start point.

Roland F
  • 3,534
  • 1
  • 2
  • 10
  • 1
    Do you see the Ulrich Neumann's answer who said that so many blue line are also the solution for that equation? – Y. zeng Dec 04 '23 at 13:15