6

I have the following complex function:

$$g (z) = (1 - a^2/z) (1 - 1 /z),$$

where $0 < a < 1$.

Calculations show that $\sqrt{g(z)}$ has a branch cut along $a^2 \to 1$. Is there a way to visualize the Riemann surface of this function and the corresponding branch cut?

Thanks for any help!

2 Answers2

5

Do you mean something like this (for a=1/2)?

ComplexPlot[Sqrt[(1 - (1/2)^2/z) (1 - 1/z)], {z, -(1/4) - (3 I)/4, 
  5/4 + (3 I)/4}]
ComplexPlot3D[Sqrt[(1 - (1/2)^2/z) (1 - 1/z)], {z, -(1/4) - (3 I)/4, 
  5/4 + (3 I)/4}, PlotRange -> {0, 10}]

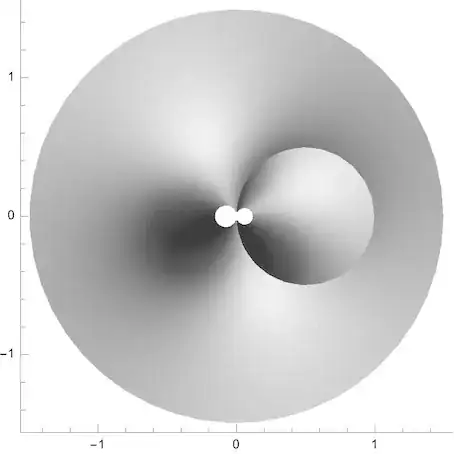
enter image description here

enter image description here

Branch cuts are depicted by black line and circle.

Manipulate[
 ComplexPlot[
  Sqrt[(1 - a^2/z) (1 - 1/z)], {z, -(1/4) - (3 I)/4, 5/4 + (3 I)/4}, 
  Epilog -> {Line[{{a^2, 0}, {1, 0}}], 
    Circle[{a^2/(1 + a^2), 0}, a^2/(1 + a^2)], Point[{0, 0}]}], {a, 0, 2}]

enter image description here

Update:

Branch cuts are definition dependent.

Your function can be factored to:

$$\sqrt{\left(1-\frac{1}{z}\right) \left(1-\frac{a^2}{z}\right)}=\sqrt{\frac{(z-1) \left(z-a^2\right)}{z^2}}$$

Sqrt[(1 - a^2/z) (1 - 1/z)] == Sqrt[((-1 + z) (-a^2 + z))/z^2] // FullSimplify

True

If you now separate the square root into two separate roots like the following you get a different branch cut (voila!, without the circular branch cut):

$$\sqrt{\frac{z-1}{z}} \sqrt{\frac{z-a^2}{z}}$$

a = 1/2;
ComplexPlot[
 Sqrt[(-1 + z)/z] Sqrt[(-a^2 + z)/z], {z, -(1/4) - (3 I)/4, 
  5/4 + (3 I)/4}]
Clear[a]

enter image description here

azerbajdzan
  • 15,863
  • 1
  • 16
  • 48
  • @Akbar: Branch cuts are dependent on the definition of your multi-function. This is how your function is defined in Mathematica. If you have different definition than Mathematica then also branch cut will be different. – azerbajdzan Dec 20 '23 at 16:57
  • @Akbar: As I said branch cuts are definition dependent. You can move branch cut anywhere you want. For example you can define square root in such a way that the branch cut will not be on the negative real axis but, say, on positive imaginary axis (or somewhere else). – azerbajdzan Dec 20 '23 at 17:18
  • @Akbar: I updated my answer with another branch cut that is what you are probably looking for, but notice that I had to change your definition of the same multi-function. – azerbajdzan Dec 20 '23 at 17:31
  • @Akbar: No, from a^2 to 1 Can't you see???? It is clear from the last image. – azerbajdzan Dec 20 '23 at 18:34
  • 1
    @Akbar: My version is 13.0.1. – azerbajdzan Dec 20 '23 at 18:37
3

With a = 1:

 f = Sqrt[(1 - 1^2/z) (1 - 1/z)];

n = 1.2;


ComplexContourPlot[ReIm @ f, {z, -n - n I, n + n I},
 Contours -> 30,
 Epilog -> Line[{{1, -5}, {1, 5}}],
 ExclusionsStyle -> Red]

enter image description here

Riemann = ResourceFunction["RiemannSurfacePlot3D"];

Riemann[f == w, Re[w], {z, w},
 Background -> GrayLevel[0.25],
 Boxed -> False,
 Lighting -> "Neutral",
 PlotPoints -> 48,
 PlotStyle -> GrayLevel[0.7]]

enter image description here

Riemann[f == w, Re[w], {z, w},
 Axes -> {True, True, False},
 Boxed -> False,
 Lighting -> "Neutral",
 PlotPoints -> 48,
 PlotStyle -> GrayLevel[0.7],
 ViewPoint -> {0, 0, 100}]

enter image description here

eldo
  • 67,911
  • 5
  • 60
  • 168
  • The red circle denotes exclusions - points where function values cannot be calculated (ComplexInfinity etc) – eldo Dec 20 '23 at 10:18
  • You can plug in different values for a (0.1, 0.5, 0.9) easily yourself and see how the ComplexContourPlot changes. – eldo Dec 20 '23 at 10:25
  • You should also plot the Riemann surface for the imaginary part. Replace Re[w] with Im[w] – eldo Dec 20 '23 at 10:38