Unexpected result for Poisson problem on torus (using PeriodicBoundaryCondition)

Question

I want to solve the Laplace problem $-\Delta u=f$ ("analyst's Laplacian") for a given $f$ and unknown $u$ on the torus $[0,2\pi]/\sim$, i.e. a rectangle with opposite sides identified. The solution is unique if one imposes $u(0,0)=0$. As a test I chose $f(x,y)=\sin(x)$. I modified code from the documentation and now have the following code:

ufun=NDSolveValue[{-Laplacian[u[x,y],{x,y}]==Sin[ x],DirichletCondition[u[x,y]==0,x==0&&y==0],PeriodicBoundaryCondition[u[x,y],0<=y<=2 Pi&&x==2 Pi,FindGeometricTransform[{{0,0},{0,2 Pi}},{{2 Pi,0},{2 Pi,2 Pi}}][[2]]],PeriodicBoundaryCondition[u[x,y],0<=x<=2 Pi&&y==2 Pi,FindGeometricTransform[{{0,0},{2 Pi,0}},{{0,2 Pi},{2 Pi,2 Pi}}][[2]]]},u,{x,y}\[Element]Rectangle[{0,0},{2Pi,2 Pi}]];
Plot3D[ufun[x,y],{x,y}\[Element]Rectangle[{0,0},{2 Pi,2 Pi}]]

The result is the following plot:

This is unexpected for me, because the solution to the equation $-\Delta u=\sin(x)$ with $u(0,0)=0$ is $u(x,y)=\sin(x)$. That is different from the plot. What went wrong?

Answer 1

New answer (06 Jan 2024)

My old answer was not clean about the way the unicity of the solution is imposed with a Dirichlet condition.

Here is a clean approach :

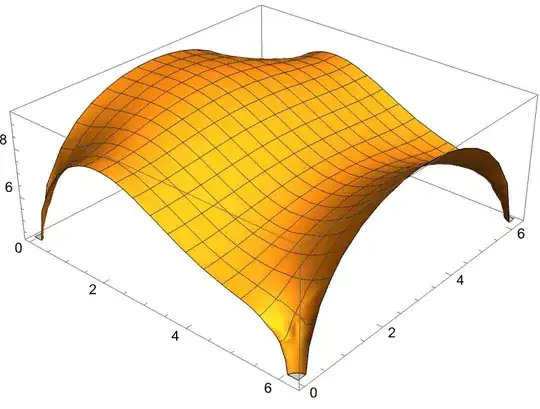
It imposes the solution to be 0 at a arbitrary point called dirichletConditionPoint which is randomly taken to be at position {4,4}. The point is the small black ball in the graphic. One can impose a value different from 0, but in this case the value would be different from the specified value (this is normal)

Get["NDSolve`FEM`"]
dirichletConditionPoint = {4, 4};
offset = 1;
myBoundaryMesh = 
  ToBoundaryMesh[Rectangle[{-offset, -offset}, {2 Pi, 2 Pi}], 
   "IncludePoints" -> {dirichletConditionPoint }];
myMesh = ToElementMesh[myBoundaryMesh];
ufun = NDSolveValue[{-Laplacian[u[x, y], {x, y}] == Sin[x]
    , DirichletCondition[u[x, y] == 0, 
     Norm[{x, y} - dirichletConditionPoint] < 10^-3]
    , PeriodicBoundaryCondition[u[x, y], x == 2 Pi, 
     TranslationTransform[{-2 Pi, 0}]]
    , PeriodicBoundaryCondition[u[x, y], y == 2 Pi, 
     TranslationTransform[{0, -2 Pi}]]
    , PeriodicBoundaryCondition[u[x, y], x == -offset, 
     TranslationTransform[{2 Pi, 0}]]
    , PeriodicBoundaryCondition[u[x, y], y == -offset, 
     TranslationTransform[{0, 2 Pi}]]}
   , u
   , {x, y} [Element] myMesh];
Show[
 Plot3D[ufun[x, y], {x, y} [Element] myMesh]
 , Graphics3D[{Black, 
   Ball[Append[dirichletConditionPoint, 
     Apply[ufun, dirichletConditionPoint]], .2]}]]

Old answer

Here is the very triky approach I explain in this answer :

https://mathematica.stackexchange.com/a/174514/5467

There is one more difficulty : Without any Dirichlet condition the solution is unique up to a constant.
With a Dirichlet condition on a small part of the boundary, it works :

offset = 1;
ufun = NDSolveValue[{-Laplacian[u[x, y], {x, y}] == Sin[x], 
    DirichletCondition[
     u[x, y] == -offset, -offset < x < -offset + .2 && y == -offset], 
    PeriodicBoundaryCondition[u[x, y], x == 2 Pi, 
     TranslationTransform[{-2 Pi, 0}]
    (* TranslationTransform[{-2 Pi, 0}] is equivalent to OP's code but is cleaner *)],
    PeriodicBoundaryCondition[u[x, y], y == 2 Pi, 
     TranslationTransform[{0, -2 Pi}]],
    PeriodicBoundaryCondition[u[x, y], x == -offset, 
     TranslationTransform[{2 Pi, 0}]], 
    PeriodicBoundaryCondition[
     u[x, y], (x > -offset + .3) && y == -offset, 
     TranslationTransform[{0, 2 Pi}]]
    }, u, {x, y} [Element] 
    Rectangle[{-offset, -offset}, {2 Pi, 2 Pi}]];
Plot3D[ufun[x, y], {x, y} [Element] Rectangle[{0, 0}, {2 Pi, 2 Pi}]]

Notice that the restriction of my extended domain [-1,2 Pi]X[-1,2 Pi] to your domain [0,2 Pi]X[0,2 Pi] is exactly periodic in your domain.

Disclaimer : I'm not a specialist. There may be problems due to the topology of the domain. Nevertheless I think that the code is worth to be shared.

Answer 2

The inhomogenity $\sin x$ is a local sink and source term.

The solution yields a current on the torus between the positive and negative areas of $\sin$.

To clamp down the potential at a point in the corners, is somehow an artefact, that generates infinite current densities.

Do VectorPlot of the Gradient without and with Dirichlet.

From physical reasons, a contact with constant potential has to have a finite contact lenght in order to generate a regular solution. Experiment with a line segment and a circle of constant potential in the center.