Mathematica can not recognize the wanted element in a matrix when doing a numeric integral, even though it is plotted on the last step?

Question

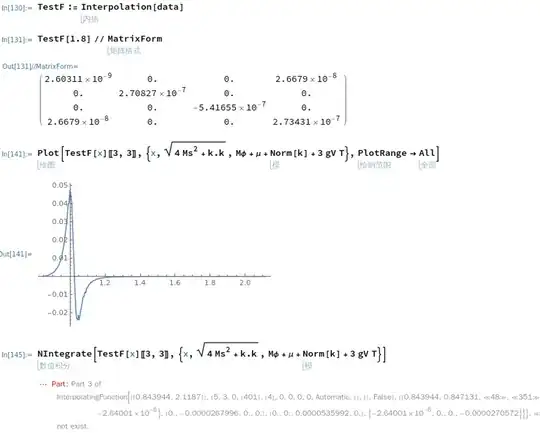
As shown, function 'TestF' is defined via interpolation and maps a number to a 4 by 4 matrix. Its (3,3) element is plotted at step 141, but not recognized in the numeric integration within the same range. How can that be possible?

The code with shorten data is following:

data={{0.843944, {{-3.4671*10^-17, 0., 
0., -3.5534*10^-16}, {0., -3.60717*10^-15, 0., 0.}, {0., 0., 
7.21434*10^-15, 0.}, {-3.5534*10^-16, 0., 
0., -3.64184*10^-15}}}, {0.907682, {{-0.0000120049, 0., 
0., -0.000123037}, {0., -0.00124899, 0., 0.}, {0., 0., 0.00249798,
 0.}, {-0.000123037, 0., 
0., -0.00126099}}}, {0.97142, {{-0.000106935, 0., 
0., -0.00109597}, {0., -0.0111256, 0., 0.}, {0., 0., 0.0222511, 
0.}, {-0.00109597, 0., 0., -0.0112325}}}, {1.03516, {{0.000101995,
 0., 0., 0.00104534}, {0., 0.0106115, 0., 0.}, {0., 
0., -0.0212231, 0.}, {0.00104534, 0., 0., 
0.0107135}}}, {1.0989, {{0.0000295598, 0., 0., 0.000302955}, {0., 
0.0030754, 0., 0.}, {0., 0., -0.0061508, 0.}, {0.000302955, 0., 
0., 0.00310496}}}, {1.16263, {{5.68556*10^-6, 0., 0., 
0.0000582707}, {0., 0.000591525, 0., 0.}, {0., 0., -0.00118305, 
0.}, {0.0000582707, 0., 0., 
0.000597211}}}, {1.22637, {{1.72719*10^-6, 0., 0., 
0.0000177018}, {0., 0.000179697, 0., 0.}, {0., 0., -0.000359394, 
0.}, {0.0000177018, 0., 0., 
0.000181424}}}, {1.29011, {{6.33575*10^-7, 0., 0., 
6.49344*10^-6}, {0., 0.0000659171, 0., 0.}, {0., 0., -0.000131834,
 0.}, {6.49344*10^-6, 0., 0., 
0.0000665507}}}, {1.35385, {{2.62468*10^-7, 0., 0., 
2.69001*10^-6}, {0., 0.0000273072, 0., 0.}, {0., 
0., -0.0000546143, 0.}, {2.69001*10^-6, 0., 0., 
0.0000275696}}}, {1.41758, {{1.2021*10^-7, 0., 0., 
1.23202*10^-6}, {0., 0.0000125067, 0., 0.}, {0., 
0., -0.0000250133, 0.}, {1.23202*10^-6, 0., 0., 
0.0000126269}}}, {1.48132, {{5.84518*10^-8, 0., 0., 
5.99067*10^-7}, {0., 6.08132*10^-6, 0., 0.}, {0., 
0., -0.0000121626, 0.}, {5.99067*10^-7, 0., 0., 
6.13978*10^-6}}}, {1.54506, {{3.00555*10^-8, 0., 0., 
3.08036*10^-7}, {0., 3.12697*10^-6, 0., 0.}, {0., 
0., -6.25395*10^-6, 0.}, {3.08036*10^-7, 0., 0., 
3.15703*10^-6}}}, {1.6088, {{1.56645*10^-8, 0., 0., 
1.60544*10^-7}, {0., 1.62974*10^-6, 0., 0.}, {0., 
0., -3.25948*10^-6, 0.}, {1.60544*10^-7, 0., 0., 
1.6454*10^-6}}}, {1.67253, {{8.4205*10^-9, 0., 0., 
8.63009*10^-8}, {0., 8.76069*10^-7, 0., 0.}, {0., 
0., -1.75214*10^-6, 0.}, {8.63009*10^-8, 0., 0., 
8.84489*10^-7}}}, {1.73627, {{4.6251*10^-9, 0., 0., 
4.74022*10^-8}, {0., 4.81195*10^-7, 0., 0.}, {0., 
0., -9.62391*10^-7, 0.}, {4.74022*10^-8, 0., 0., 
4.8582*10^-7}}}, {1.80001, {{2.60284*10^-9, 0., 0., 
2.66763*10^-8}, {0., 2.708*10^-7, 0., 0.}, {0., 0., -5.416*10^-7, 
0.}, {2.66763*10^-8, 0., 0., 
2.73403*10^-7}}}, {1.86375, {{1.48338*10^-9, 0., 0., 
1.5203*10^-8}, {0., 1.54331*10^-7, 0., 0.}, {0., 
0., -3.08662*10^-7, 0.}, {1.5203*10^-8, 0., 0., 
1.55814*10^-7}}}, {1.92749, {{8.54432*10^-10, 0., 0., 
8.75699*10^-9}, {0., 8.88951*10^-8, 0., 0.}, {0., 
0., -1.7779*10^-7, 0.}, {8.75699*10^-9, 0., 0., 
8.97496*10^-8}}}, {1.99122, {{4.97424*10^-10, 0., 0., 
5.09805*10^-9}, {0., 5.1752*10^-8, 0., 0.}, {0., 
0., -1.03504*10^-7, 0.}, {5.09805*10^-9, 0., 0., 
5.22495*10^-8}}}, {2.05496, {{2.92371*10^-10, 0., 0., 
2.99648*10^-9}, {0., 3.04183*10^-8, 0., 0.}, {0., 
0., -6.08366*10^-8, 0.}, {2.99648*10^-9, 0., 0., 
3.07107*10^-8}}}, {2.1187, {{1.72959*10^-10, 0., 0., 
1.77264*10^-9}, {0., 1.79947*10^-8, 0., 0.}, {0., 
0., -3.59894*10^-8, 0.}, {1.77264*10^-9, 0., 0., 1.81677*10^-8}}}};
TestF:=Interpolation[data];
Plot[TestF[x][[3, 3]], {x, Sqrt[4 Ms^2 + k.k], M\[Phi] + \[Mu] + Norm[k] + 3 gV T}, PlotRange -> All]
NIntegrate[TestF[x][[3, 3]], {x, Sqrt[4 Ms^2 + k.k], M[Phi] + [Mu] + Norm[k] + 3 gV T}]

Answer 1

Since you did not provide the values for the several constants, I will use the {xmin, xmax} from the data for both plotting and integration.

    {xmin, xmax} = MinMax[data[[All, 1]]]
(* {0.843944, 2.1187} *)

Plot[TestF[x][[3, 3]], {x, xmin, xmax},
 PlotRange -> All]

    NIntegrate[TestF[x][[3, 3]], {x, xmin, xmax},
     MaxRecursion -> 20]

The warning message indicates that an integration was attempted before x was given a numeric value. After the symbolic integration failed, the numeric integration provided the result. To avoid the initial attempt at integration with symbolic x, define

    f[x_?NumericQ] := TestF[x][[3, 3]]

Then there is no warning message:

    NIntegrate[f[x], {x, xmin, xmax},
     MaxRecursion -> 20]
(* -0.000527017 *)