Find height of oscillating solution from NDSolve

Question

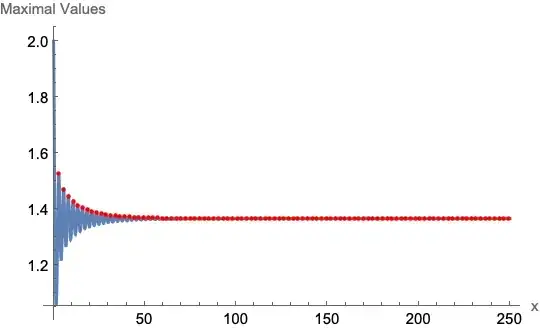
There are a class of differential equations whose solution oscillates around some equilibrium indefinitely after settling down. Below is an implementation of such an equation

t0 = 10^-6; tf = 50;
y0 = 2; dy0 = 0;
sol = NDSolve[{y''[t] == -(0.1 + 1/t) y'[t] - 1 + 6*y[t]^2 - 4 y[t]^3, 
               y[t0] == y0, y'[t0] == dy0}, {y}, {t, t0, tf}];

which produces an oscillating solution around y = 1.3.

I'd like to do two things. First, I'd like to stop the integration once a steady-state equilibrium is achieved. Second, I would like the find the midpoint of the oscillations, i.e., the height (for this, I could simply average over the late-time solutions so it's less of a problem).

In more complicated problems, the frequency might be increasing indefinitely, but the equilibrium height remains the same. I would hope to be able to accommodate this in the final solution.

Is there a way to easily achieve this using WhenEvent or something similar?

You can use the Hilbert transform to shift the oscillation by a half-period. Take then square root of the sum of squares to obtain the envelope, https://mathematica.stackexchange.com/a/49081/9469 — yarchik, Jan 06 '24 at 13:39

Ulrich Neumann · Answer 1 · 2024-01-06T08:49:23.617

3

The possible stationary values (y'[t]==0,y''[t]==0) from your ode follow from

asy = Values@Solve[-1 + 6*y[t]^2 - 4 y[t]^3 == 0, y[t], Reals] //Flatten
asy//N (*{0.5, -0.366025, 1.36603}*)

To realize WhenEvent try (I have increased the value of tf)

t0 = 10^-6; tf = 250;
y0 = 2; dy0 = 0;
Y = NDSolveValue[{y''[t] == -(0.1 + 1/t) y'[t] - 1 + 6*y[t]^2 - 
      4 y[t]^3, y[t0] == y0, y'[t0] == dy0, 
    WhenEvent[
     RealAbs[ y'[t]] < 0.001` && RealAbs[y[t] - asy[[3]]] < .001 , 
     "StopIntegration"]}, y , {t, t0, tf}];
Plot[Y[t], {t, t0, Y["Domain"][[1, 2]]}, PlotRange -> All, 
 GridLines -> {None, grid}]

addendum

For the case you have no apriori information about the asymptotes check condition |D[y[t]^2,t]| <<1

Try

Y = NDSolveValue[{y''[t] == -(0.1 + 1/t) y'[t] - 1 + 6*y[t]^2 - 
      4 y[t]^3, y[t0] == y0, y'[t0] == dy0, 
    WhenEvent[   RealAbs[y[t] y'[t]] < .000001 , "StopIntegration"]}, 
   y , {t, t0, tf}];
Plot[Y[t], {t, t0, Y["Domain"][[1, 2]]}, PlotRange -> All, 
 GridLines -> {None, grid}]

edited Jan 06 '24 at 08:49

answered Jan 05 '24 at 11:49

Ulrich Neumann

53,729
2
23
55

Thank you for the solution. However, I am more interested in the abstract case where one can't necessarily use the differential equation to deduce where the asymptotes are. Is it possible solve this without first knowing through some other means? – MarcosMFlores Jan 05 '24 at 17:07
How would you define asymptotes in general ? – Ulrich Neumann Jan 05 '24 at 17:28
The solution goes as $f(t) = c + A(t)\cos[\omega(t) + \delta]$ as the solution goes to $t\to\infty$. The asymptotes would be $c$ in this case. – MarcosMFlores Jan 08 '24 at 08:01
@MarcosMFlores Did you recognize the addendum in my answer? – Ulrich Neumann Jan 08 '24 at 09:51
I don't think the condition you specified will always work. For example, consider the function $y(t) = 2 + \cos(t^2)/(t + 1)$ for $t > 0$. The derivative of $y^2(t)$ is not small, but the function still approaches a fixed value of 2. – MarcosMFlores Jan 08 '24 at 10:40
@MarcosMFlores But the condition seems to answer what you asked for I think. – Ulrich Neumann Jan 08 '24 at 10:51

score 3 · Answer 2 · edited Jan 05 '24 at 19:42

I am not sure if I understand the question--are you looking for a way to collect the maxima? If so, you could do this:

{sol, extrema} = Reap[
  NDSolveValue[{y''[t] == -(1/10 + 1/t) y'[t] - 1 + 6*y[t]^2 - 
      4 y[t]^3, y[t0] == y0, y'[t0] == dy0, 
    WhenEvent[y'[t] == 0, Sow[{t, y[t]}]]}, y, {t, t0, tf}]
  ]

And then:

ListPlot[extrema,AxesLabel->{"x","extremal values"}]

or

ListPlot[extrema[[1, 2 ;; -1 ;; 2]],{"x","maximal values"}]
Show[
 Plot[sol[t], {t, t0, tf}, PlotRange -> All, 
  AxesLabel -> {"x", "Maximal Values"}],
 ListPlot[extrema[[1, 2 ;; -1 ;; 2]], 
  PlotStyle -> {AbsolutePointSize[2], Red}, PlotRange -> All]
 ]

Find height of oscillating solution from NDSolve

2 Answers2