Indeterminate Lyapunov exponenet for four-wing attractor

Question

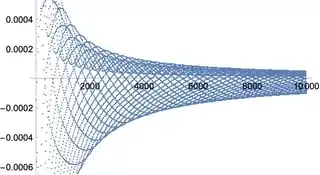
We are using Chris K's answer on another question for finding Lyapunov Exponents for a dynamical system (Four-Wing Attractor)

GramSchmidt[w_?MatrixQ] := Module[{v = ConstantArray[0, Length[w]]}, 
  Table[v[[n]] = w[[n]] - Sum[(v[[i]].w[[n]]/v[[i]].v[[i]])*v[[i]], {i, n - 1}], {n, Length[w]}]; v]
LyapunovExponents[eqnsin_List, icsin : ({__Rule} | _Association), nlein_Integer: 0, opts___?OptionQ] := Module[{
(* options *)
tstep, maxsteps, ndsolveopts, logbase, showplot, plotexponents, plotopts,
(* iterators *)
c, i, j,
(* other variables *)
δ, neq, nle, vars, rhs, jac, eqns, unks, ics, cum, res, edat, state, newstate, sol, W, norms},
(* parse options *)
tstep = Evaluate[TStep /. Flatten[{opts, Options[LyapunovExponents]}]];
maxsteps = Evaluate[MaxSteps /. Flatten[{opts, Options[LyapunovExponents]}]];
ndsolveopts = Evaluate[NDSolveOpts /. Flatten[{opts, Options[LyapunovExponents]}]];
logbase =Evaluate[LogBase /. Flatten[{opts, Options[LyapunovExponents]}]];
showplot = Evaluate[ShowPlot /. Flatten[{opts, Options[LyapunovExponents]}]];
plotexponents = Evaluate[PlotExponents /. Flatten[{opts, Options[LyapunovExponents]}]];
plotopts = Evaluate[PlotOpts /. Flatten[{opts, Options[LyapunovExponents]}]];
neq = Length[eqnsin];
If[nlein == 0, nle = neq, nle = nlein]; (* how many exponents *)
(* extract vars and right hand sides from eqnsin *)
vars = eqnsin[[All, 1, 0, 1]];
rhs = eqnsin[[All, 2]];
(* jacobian matrix *)
jac = D[rhs, {Replace[vars, {x_ -> x[t]}, 1]}];
eqns = Join[
  eqnsin,
  Flatten[Table[δ[i, j]'[t] == (jac.Table[δ[i, j][t], {i, neq}])[[i]], {j, nle}, {i, neq}]]
];
unks = Join[
  vars,
  Flatten[Table[δ[i, j], {j, nle}, {i, neq}]]
];
ics = Join[
  Table[var[0] == (var /. icsin), {var, vars}],
  Flatten[Table[δ[i, j][0] == IdentityMatrix[neq][[i, j]], {j, nle}, {i, neq}]]
];
cum = Table[0, {nle}];
state = First@NDSolve`ProcessEquations[Flatten[Join[eqns, ics]], unks, t, Evaluate[Sequence @@ ndsolveopts]];
(* main loop *)
edat = Table[
  newstate = First@NDSolveReinitialize[state, ics]; NDSolveIterate[newstate, c tstep];
  sol = NDSolve`ProcessSolutions[newstate];
W = GramSchmidt[Evaluate[Table[δ[i, j][c tstep], {j, nle}, {i, neq}] /. sol]];
  norms = Map[Norm, W];
(* update running vector magnitudes *)
  cum = cum + Log[logbase, norms];
ics = Join[
    Table[var[c tstep] == (var[c tstep] /. sol), {var, vars}],
    Flatten[Table[δ[i, j][c tstep] == (W/norms)[[j, i]], {j, nle}, {i, neq}]]
  ];
  cum/(c tstep)
, {c, maxsteps}];
If[showplot, Print[ListPlot[Transpose[edat][[1 ;; plotexponents]], Evaluate[Sequence @@ plotopts]]]];
Return[cum/(maxsteps tstep)]
];
Options[LyapunovExponents] = {NDSolveOpts -> {}, TStep -> 1, MaxSteps -> 10^4, LogBase -> E,
  ShowPlot -> False, PlotExponents -> 1, PlotOpts -> {}};

Our initial conditions and the equations are given below.

ics = {x -> 0.1, y -> 0.1, z -> 0.1};
equations= {Derivative[1][x][t] == 14 (-x[t] + y[t]) + 4 y[t] z[t], 
 Derivative[1][z][t] == x[t] y[t] - 43 z[t], 
 Derivative[1][y][t] == 8.1 x[t] + 16 y[t] - x[t] z[t]}
LyapunovExponents[equations, ics]
    {0.000634328, -3.35805, Indeterminate}

However, one of the results is Indeterminate and we are clueless about the cause.

Is there a problem in the code, or does the system genuinely an indeterminate Lyapunov exponent?

Please help us resolve the issue.

Answer 1

I think it's neither an indeterminate Lyapunov exponent nor a problem with the code, just it needs a bit more careful application. The first thing to do is to simulate the model, to get an idea of what's happening and to get good initial conditions for LyapunovExponents.

sol = NDSolve[{equations, {x[0] == 0.1, y[0] == 0.1, z[0] == 0.1}},
  {x, y, z}, {t, 0, 1000}][[1]];
Plot[Evaluate[{x[t], y[t], z[t]} /. sol], {t, 990, 1000}]
ParametricPlot3D[Evaluate[{x[t], y[t], z[t]} /. sol], {t, 990, 1000}]

Based on this, I think your system reaches a limit cycle, not a chaotic attractor. Therefore the Lyapunov exponents should be 0 (phase shift on the cycle) and two negative numbers (showing attraction to the limit cycle).

Using the final values of sol as initial conditions for LyapunovExponents helps it converge faster, which you can see with the ShowPlot option.

LyapunovExponents[equations, ics, ShowPlot -> True]
(* {0.000466946, -3.35772, Indeterminate} *)

versus

ics2 = Thread[{x, y, z} -> ({x[1000], y[1000], z[1000]} /. sol)]
LyapunovExponents[equations, ics2, ShowPlot -> True]
(* {-0.0000533646, -3.35716, Indeterminate} *) 

Notice how the first exponent got an order of magnitude closer to 0 by starting on the attractor?

Finally, about those Indeterminate values. The algorithm has to re-orthonormalize the solution to the variational equation δ periodically because the dominant exponent, well, dominates the others. You can read more about it in Wolf et al. 1985 and Sandri 1996, which were the basis of LyapunovExponents. The default value for this TStep is 1, which is too large for your system, which oscillates fairly rapidly. Reducing TStep (and increasing MaxSteps from its default of 10^4 accordingly) fixes that problem:

LyapunovExponents[equations, ics2, ShowPlot -> True, TStep -> 0.1, MaxSteps -> 10^5]
{-0.0000531121, -3.35716, -37.6428}

That -37.6428 is the problem child. If you want to doublecheck, decrease TStep again and put the kettle on (this takes like 5 minutes):

LyapunovExponents[equations, ics2, TStep -> 0.001, MaxSteps -> 10^6]
(* {0.000490278, -3.35846, -37.642} *)

Pretty similar.

If you want more accuracy in your exponents, increase MaxSteps further. If you only care about the dominant exponent, you can ask for only one exponent and get away with the default (or even larger) TStep:

LyapunovExponents[equations, ics, 1]
(* {0.000466672} *)

Even better, since the solution is periodic, you could calculate the equivalent Floquet exponents instead, which only needs integration over one period. Unfortunately I don't have code for this implemented in base Mathematica, but using my EcoEvo package I get:

(* {-2.32332*10^-7, -3.35701, -37.643} *)

which lines up well.