How can I get samples of f(x) that are roughly evenly spaced?

Question

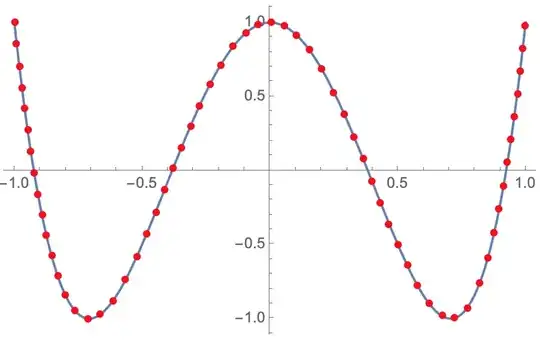
I am looking for an efficient way of getting 60 to 80 samples of an arbitrary f(x) such that the distance between adjacent samples are approximately equal. My first attempt is based on a first order approximation at different points.

f[x_]:=1-8 x^2+8 x^4;
dist=0.15;
xs=Most@NestWhileList[#+Sqrt[dist^2/(1+f'[#]^2)]&,-1.0,#<1.0&];
smpls={#,f[#]}&/@xs;
Plot[f[x],{x,-1,1},Epilog->{AbsolutePointSize@5,Red,Point[smpls]}]

In the image above, the distance between samples is too large when my algorithm gets to a value where f'[x] is close to zero. I can get much better results with my next approach.

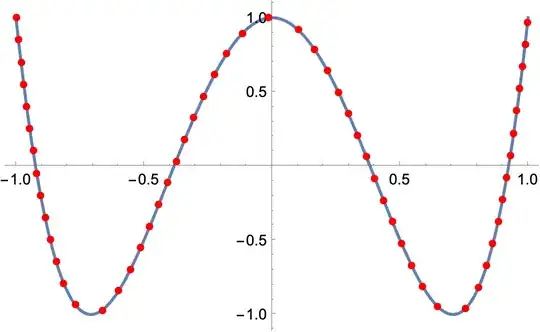
hack=2.2;
xs=Most@NestWhileList[#+Min[hack*dist^2,Sqrt[dist^2/(1+f'[#]^2)]]&,-1.0,#<1.0&];
smpls={#,f[#]}&/@xs;
Plot[f[x],{x,-1,1},Epilog->{AbsolutePointSize@5,Red,Point[smpls]}]

The spacing of the second samples are close enough to evenly spaced. The problem is that the value assigned to 'hack' should be adjusted for each example. Is there better way to make such samples of an arbitrary function?

Answer 1

f[x_] := 1 - 8  x^2 + 8  x^4;

You can use the option MeshFunctions -> {ArcLength} and ...

1.

Specify the number of equal-arc-length segments

numberofsegments = 60;
mesh1 = numberofsegments - 1;
plt1 = Plot[f @ x, {x, -1, 1},
  MeshFunctions -> {ArcLength}, 
  Mesh -> mesh1, 
  MeshStyle -> Directive[PointSize @ Medium, Red], 
  MeshShading -> {Green, Blue}]

Verify that we get 60 equal-arc-length line segments:

{Length @ #, Counts @ N @ Round[#, 10^-3]} & @
 Cases[plt1, l : Line[{__List}] :> ArcLength @ l, All]

{60, <|0.14 -> 60|>}

2.

Specify segment length

dist = 0.15;
al = N @ ArcLength[f[x], {x, -1, 1}];
mesh2 = {Range[0, al, dist]/al};
plt2 = Plot[f @ x, {x, -1, 1}, 
  MeshFunctions -> {ArcLength}, 
  Mesh -> mesh2, 
  MeshStyle -> Directive[PointSize @ Medium, Red], 
  MeshShading -> {Green, Blue}]

Verify that all line segments (except the last one) has arc length dist:

{Length @ #, Counts @ N @ Round[#, 10^-3]} & @
 Cases[plt2, l : Line[{__List}] :> ArcLength @ l, All]

{57, <|0.15 -> 56, 0.029 -> 1|>}

Answer 2

• If we want to the ArcLength approximately equal to the dist = 0.15;, we can define an arclength function arclength which satisfies the differential equation arclength'[x] == Sqrt[1 + D[f[x], x]^2].

Clear[f, dist, sol, times];
f[x_] := 1 - 8  x^2 + 8  x^4;
dist = 0.15;
{sol, times} = 
  NDSolve[{y'[x] == D[f[x], x], y[-1] == f[-1], 
     arclength'[x] == Sqrt[1 + D[f[x], x]^2], arclength[-1] == 0, 
     WhenEvent[Mod[arclength[x], dist] == 0, Sow[x]]}, {y, 
     arclength}, {x, -1, 1}] // Reap;
Plot[y[x] /. sol, {x, -1, 1}, Mesh -> times, MeshStyle -> Red, 
 MeshShading -> {Green, Blue}]

Answer 3

$Version

(* "14.0.0 for Mac OS X ARM (64-bit) (December 13, 2023)" *)

Clear["Global`*"]

f[x_] := 1 - 8  x^2 + 8  x^4;

dist = 0.15;

length = ArcLength[{x, f[x]}, {x, -1, 1}] // N

(* 8.42921 *)

The following calculation is quite slow

xval[len_?NumericQ] := xv /. FindRoot[
   ArcLength[{x, f[x]}, {x, -1, xv}] == len, {xv, 
    Rescale[len, {0, length}, {-1, 1}]}]
xvalues = Prepend[xval /@ Range[dist, length, dist], -1];
Plot[f[x], {x, -1, 1},
 Epilog -> {AbsolutePointSize@5, Red,
   Point[{#, f[#]} & /@ xvalues]}]

Answer 4

• To contain the boundary points, we can use MeshFunctions -> {0 &, "ArcLength"} and Subdivide[numberofsegments].

Clear["Global`*"];
f[x_] := 1 - 8  x^2 + 8  x^4;
numberofsegments = 60;
{xmin, xmax} = {-1, 1};
plt1 = Plot[f@x, {x, xmin, xmax}, MeshFunctions -> {0 &, "ArcLength"},
   Mesh -> {Subdivide[numberofsegments]}, MeshStyle -> Red]

Answer 5

I thought an implementation with equal ArcLength between samples would be slow, so I was planning to use equal EuclideanDistance instead. I came up with the code below that uses equal EclideanDistance.

f[x_]:=1-8 x^2+8 x^4;
dist=0.15;
nextX[f_,x1_]:=With[{y1=f[x1]},x/.FindRoot[(x1-x)^2+(y1-f[x])^2-dist^2,{x,x1,x1+dist}]];
xs=NestWhileList[nextX[f,#]&,-1,(-1<=#<=1)&];
samples={#,f@#}&/@xs;
Plot[f[x],{x,-1,1},Epilog->{Red,AbsolutePointSize@4,Point@samples},PlotLabel->"Equal EuclideanDistance"]

The EuclideanDistance between all adjacent samples above 0.15, but it seems we should have additional samples near the local min/max of f[x]. The implementation below is based on the solution from kglr, and uses equal ArcLength. I guess I wasn't clear that the result of the algorithm should be a matrix of points. The graphics are just a way of showing what the points look like. The solution by kglr didn't include samples at each end point, and my code below compensates for that.

numberofsegments=60;
{xmin,xmax}={-1,1};
plt1=Plot[f@x,{x,xmin,xmax},MeshFunctions->{ArcLength},Mesh->numberofsegments-2];
coords=First@Cases[plt1,GraphicsComplex[lst_List,__]:>lst,{2,-8}];
samples=Part[coords,First@Cases[plt1,Point[lst_List]:>lst,{6,-3}]];
samples=SortBy[Join[{{xmin,f@xmin},{xmax,f@xmax}},samples],First];
Plot[f[x],{x,xmin,xmax},Prolog->{AbsolutePointSize@4,Red,Point@samples},PlotLabel->"Equal ArcLength"]

Both solutions above are fairly fast, but the second approach meets my needs much better.