Two-directional vibration of Euler–Bernoulli beam with Lagrange multiplier

Question

Background

I'm going to investigate a beam-pendulum coupling system (in this question I won't consider the pendulum though), that is, a spherical pendulum is suspended on the tip of a cantilever beam. therefore it may be essential to write the vibrational displacement in two functions, which are constrained by inextensibility of the beam.

I'm following this article, which starts from a Lagrangian with a Lagrange multiplier.

https://doi.org/10.1119/10.0001389

I upload 2 pages of this paper here.

I've set $T_1,T_2=0$ to ignore effects from pendulum etc., i.e. there is the beam only.

PDE

(* PDE *)
eqn = {
  \[Mu] Derivative[2,0][u][t,s] + c Derivative[1,0][u][t,s] - D[\[Lambda][t, s](1+Derivative[0,1][u][t,s]), s] == 0,
  \[Mu] Derivative[2,0][v][t,s] + c Derivative[1,0][v][t,s] - D[\[Lambda][t, s]Derivative[0,1][v][t,s], s] +
    EI(D[(1+Derivative[0,1][v][t,s]^2+Derivative[0,1][v][t,s]^4)Derivative[0,2][v][t,s], {s, 2}] +
    D[(1+Derivative[0,1][v][t,s]^2/2)Derivative[0,2][v][t,s]^2, s]) == 0
}
(* Boundary Condition *)
bcrhs = D[(1+D[v[t,s], s]^2+D[v[t,s], s]^4)D[v[t,s], s, s], s] + (1+D[v[t,s], s]^2/2)D[v[t,s], s, s]^2 /. s->l
bc = {
  u[t, 0] == 0,
  Derivative[0, 1][u][t, l] == -1,
  v[t, 0] == 0,
  Derivative[0, 1][v][t, 0] == 0,
  Derivative[0, 2][v][t, l] == 0,
  [Lambda][t, l]Derivative[0, 1][v][t, l] == EI bcrhs
};
(* Initial Condition, a trivial one though *)
ic = {
  u[0, s] == 0,
  Derivative[1, 0][u][0, s] == 0,
  v[0, s] == 0,
  Derivative[1, 0][v][0, s] == 0
}
(* Constraint *)
constraint = (1+Derivative[0,1][u][t,s])^2+Derivative[0,1][v][t,s]^2==1
(* Parameters *)
l = 1;
EI = 1;
[Mu] = 1;
c = 1;

My attempts

I've tried manual discretization of PDEs and BCs for spatial variable $s$(with the help of pdetoode from 127997). Redundant ODEs are removed (2 of u, 4 of v). Finally I got a correct amount of DEs, which is $2m$ where $m$ is the grid size.

For the constraint, as its sign is not fixed, it cannot be directly solved. Thus I followed the instruction of the wiki, differentiated the constraint for 2 times and substituted high-order derivatives by terms including $\lambda$ to obtain a constraint with $\lambda$. Then differentiate it once more to obtain a DE version constraint.

For the initial condition for the DE version constraint, I don't know what to do. After substitute ICs into the constraint equation with $\lambda$, I got a equation which evaluates to True. Thus, being inspired by some observation of arbitrariness, I tried to set constraint IC $\lambda(0,s)=0$. Then it's discretized to $m$ ICs.

Finally, I got $2m$ second order ODEs, $m$ first order ODEs, and $5m$ initial conditions. When I throw them into NDSolve(without set any option), it says:

1. NDSolve::parpiv: Zero pivot was detected during the numerical factorization or there was a problem in the iterative refinement process. It is possible that the matrix is ill-conditioned or singular.
2. NDSolve::ivres: NDSolve has computed initial values that give a zero residual for the differential-algebraic system, but some components are different from those specified. If you need them to be satisfied, giving initial conditions for all dependent variables and their derivatives is recommended.
3. NDSolve::index: The DAE solver failed at `t` = `0`. The solver is intended for index 1 DAE systems and structural analysis indicates that the DAE index is `3`. The option Method->{"IndexReduction"->Automatic} may be used to reduce the index of the system.

Set Method -> {"IndexReduction" -> True} gives NDSolve::ivres and NDSolve::nderr.

My question

I want to know what's the correct way to solve this PDE system. (Use built-in discretizer is also OK, but I'm afraid that it may be not so handy for introduce the pendulum coupling)

If you think that my code for attempts is a needed info, please comment.

Answer 1

To solve this problem we can use FDM code based on explicit Verlet step for the pendulum bob motion and implicit algorithm for the cantilever beam deformation. We use standard simplification to derive parameters $u,\lambda$ from equations (3) and (8) in a form

$u_s=\sqrt{1-v_s^2}-1, u=\int_0^su_sds$

$\lambda (1+u_s)=\lambda_0+\int_0^s(\mu u_{tt}+c u_t)ds$

Note that code with $\lambda(t,s)$ in a form above is terribly slow, while numerical results are not differ from that computed with $\lambda(t)$ only. Therefore we use simplified code as follows

(*Parameters *)
l = .815; n = 15; h = l/(n - 1);
EI = .096; g = 9.8;
[Mu] = 8.41 10^-3; mp = 0.033; R = 0.225; gamma = 2.02;
c = 1.51 10^-2; cp = 5.31 10^-4; alpha = 42/180 Pi;
dt = 5 10^-2; tmax = 20;
sgrid = Range[0, l, h];
tgrid = Range[0, tmax, dt]; jmax = nt = Length[tgrid]; nn = 
 Length[sgrid]; ds = 
 Table[NDSolve`FiniteDifferenceDerivative[i, sgrid, 
    "DifferenceOrder" -> 4]["DifferentiationMatrix"], {i, 4}];
U = Array[uu, {nn, nt}]; V = Array[vv, {nn, nt}]; lambda = 
 Array[ll, {nn, nt}]; lambda0 = Array[ll0, {nt}]; xp = 
 Array[xx, {nt}]; yp = Array[yy, {nt}]; zp = Array[zz, {nt}]; T1 = 
 Array[tt1, {nt}]; T2 = Array[tt2, {nt}]; Vpx = 
 Array[vpx, {nt}]; Vpy = 
 Array[vpy, {nt}]; fu = -T2 Cos[alpha] + T1 xp/R;(External force fu)
fv = -T2 Cos[alpha] V[[-1, All]]/l + T1 yp/R;(External force fv)
us = Sqrt[1 - (ds[[1]] . V)^2] - 1;(inextensibility constraint)
Do[uu[i, j] = 
    If[i == 1, 0, 
     h/2 Sum[(us[[k - 1, j]] + us[[k, j]]), {k, 2, i}]];, {i, nn}, {j,
    nt}];(u[t,s]= Integrate[us,{x,0,s}] )
lambda0 = fu/(1 + us[[-1, All]]);
(the Lagrange multiplier 

[Lambda](t,s)=[Lambda]0(t)+Integrate[[Mu] D[u[t,x],t,t]+c 

D[u[t,x],t],{x,s,l}]/(1+D[u[t,s],s]))
bcrhs[j_] := (1 + 1/2 (ds[[1]] . V[[All, j]])^2) (ds[[2]] . 
      V[[All, j]])^2 + 
   ds[[2]] . 
     V[[All, j]] (2 ds[[1]] . V[[All, j]] ds[[2]] . V[[All, j]] + 
      4 (ds[[1]] . V[[All, j]])^3 ds[[2]] . 
        V[[All, j]]) + (1 + (ds[[1]] . V[[All, j]])^2 + (ds[[1]] . 
        V[[All, j]])^4) ds[[3]] . V[[All, j]];
(Initial Condition){x0, vx0, y0, vy0} = {.0, .1, 0, 
  0.01}; z0 = -Sqrt[R^2 - x0^2 - y0^2];
Do[uu[i, 1] = 0; uu[i, 2] = 0; vv[i, 1] = 0; 
 vv[i, 2] = 0;, {i, nn}]; Do[xx[i] = x0; vpx[i] = vx0; yy[i] = y0; 
 vpy[i] = vy0; zz[i] = z0; tt1[i] = -mp g R/z0; 
 tt2[i] = mp g/Sin[alpha], {i, 2}]; ll0[1] = -tt2[1] Cos[alpha]; 
ll0[2] = -tt2[2] Cos[alpha];
test = Table[.1, {nn}];
Do[(Verlet explicit step)
  fx = If[j <= 2, 0, 
    mp (U[[-1, j]] + U[[-1, j - 2]] - 2 U[[-1, j - 1]])/dt^2 + 
     cp (U[[-1, j]] - U[[-1, j - 1]])/dt ]; 
  fy = If[j <= 2, 0, 
    mp (V[[-1, j]] + V[[-1, j - 2]] - 2 V[[-1, j - 1]])/dt^2 + 
     cp (V[[-1, j]] - V[[-1, j - 1]])/dt ];
  xx[j + 1] = 
   xx[j] + vpx[j] dt - (fx + cp vpx[j] + tt1[j] xx[j]/R) dt^2/2 ; 
  vpx[j + 1] = vpx[j] - (fx + cp vpx[j] + tt1[j] xx[j]/R) dt; 
  yy[j + 1] = 
   yy[j] + vpy[j] dt - (fy + cp vpy[j] + tt1[j] yy[j]/R) dt^2/2 ; 
  vpy[j + 1] = vpy[j] - (fy + cp vpy[j] + tt1[j] yy[j]/R) dt;
  zz[j + 1] = -Sqrt[R^2 - xx[j + 1]^2 - yy[j + 1]^2]; 
  tt1[j + 1] = -R/
     zz[j + 1] (mp g + (mp (zz[j + 1] + zz[j - 1] - 2 zz[j])/dt^2 + 
        cp /dt/2 (zz[j + 1] - zz[j - 1])));
  tt2[j + 1] = -tt1[j + 1] zz[j + 1]/R/ Sin[alpha];
  (beam implicit step)
  r2 = EI ds[[1]] . bcrhs[j + 1] - 
    lambda0[[j + 1]] (ds[[2]] . V[[All, j + 1]]);
  eq2 = [Mu] (V[[All, j + 1]] + V[[All, j - 1]] - 2 V[[All, j]]) + 
    c dt/2 (V[[All, j + 1]] - V[[All, j - 1]]) + dt^2 r2;
  eqs = Table[Drop[Drop[eq2, 2], -2][[i]] == 0, {i, nn - 4}]; 
  varAll = V[[All, j + 1]]; 
  bC0 = {(ds[[1]] . V[[All, j + 1]])[[1]] == 0, V[[1, j + 1]] == 0}; 
  bC1 = {lambda0[[j + 1]] (ds[[1]] . V[[All, j + 1]])[[-1]] - 
      EI bcrhs[j + 1][[-1]] == 
     fv[[j + 1]], (ds[[2]] . V[[All, j + 1]])[[-1]] == 0}; 
  eqAll = Join[eqs, bC0, bC1]; 
  ini = Table[{varAll[[i]], test[[i]]}, {i, Length[varAll]}]; 
  sol = Quiet@
    FindRoot[eqAll, ini, 
     Method -> {"Newton", "StepControl" -> "TrustRegion"}, 
     MaxIterations -> 20]; test = varAll /. sol; 
  Do[vv[i, j + 1] = test[[i]], {i, nn}];, {j, 2, 
   jmax - 1}] // AbsoluteTiming

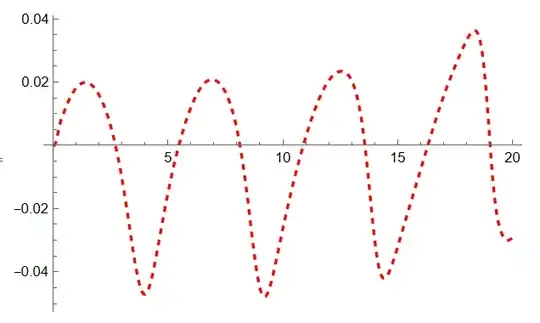
It takes about 205s on my laptop. Visualization of the cantilever beam tip and the pendulum bob movement

ListLinePlot[Transpose[{tgrid, V[[-1, All]]}], 
 PlotStyle -> {Dashed, Red}]
ListLinePlot[{Transpose[{tgrid, xp}], Transpose[{tgrid, yp}], 
  Transpose[{tgrid, zp}]}, PlotLegends -> {"x", "y", "z"}] 

Forces acting on the cantilever beam and pendulum

ListLinePlot[{Transpose[{tgrid, T1}], Transpose[{tgrid, T2}], 
  Transpose[{tgrid, fu}], Transpose[{tgrid, fv}]}, 
 PlotLegends -> {"T1", "T2", "fu", "fv"}]

Lagrange multiplier $\lambda$

ListLinePlot[Evaluate[Transpose[{tgrid, lambda0}]], 
 PlotStyle -> {Dashed, Red}]

Animation

frame3D2 = 
  Table[Show[
    Graphics3D[{Red, PointSize[Large], 
      Point[{{xp[[j]] + l, yp[[j]] + V[[-1, j]], zp[[j]]}, {0, 0, 
         0}}], Blue, 
      Line[{{l, V[[-1, j]], 0}, {xp[[j]] + l, yp[[j]] + V[[-1, j]], 
         zp[[j]]}}], Tube[{{0, 0, -l}, {0, 0, l Tan[alpha]}}, 0.05], 
      Black, Line[{{0, 0, l Tan[alpha]}, {l, V[[-1, j]], 0}}]}, 
     PlotRange -> {{0, l + R}, {-l, l}, {-l, l}}, Boxed -> False], 
    ListLinePlot3D[Table[{sgrid[[i]], V[[i, j]], 0}, {i, nn}], 
     ColorFunction -> Hue, Axes -> False]], {j, 1, jmax, 2}];
ListAnimate[frame3D2]

Update 1. With initial data {x0, vx0, y0, vy0} = {.0, .01, 0, 0.05} we have Animation

Update 2. In general case we can compute $\lambda(t,s)$ as well using integral term in the Lagrange multiplayer definition. The corresponding code is terribly slow due to FindRoot usage. Also this code is unstably at large t. In a case of transvers excitation (see Update 1) we have

(*Parameters *)
l = .815; n = 15; h = l/(n - 1);
EI = .096; g = 9.8;
[Mu] = 8.41 10^-3; mp = 0.033; R = 0.225; gamma = 2.02;
c = 1.51 10^-2; cp = 5.31 10^-4; alpha = 42/180 Pi;
dt = 5 10^-2; tmax = 15;
sgrid = Range[0, l, h];
tgrid = Range[0, tmax, dt]; jmax = nt = Length[tgrid]; nn = 
 Length[sgrid]; ds = 
 Table[NDSolve`FiniteDifferenceDerivative[i, sgrid, 
    "DifferenceOrder" -> 4]["DifferentiationMatrix"], {i, 4}];
U = Array[uu, {nn, nt}]; V = Array[vv, {nn, nt}]; lambda = 
 Array[ll, {nn, nt}]; lambda0 = Array[ll0, {nt}]; xp = 
 Array[xx, {nt}]; yp = Array[yy, {nt}]; zp = Array[zz, {nt}]; T1 = 
 Array[tt1, {nt}]; T2 = Array[tt2, {nt}]; Vpx = 
 Array[vpx, {nt}]; Vpy = 
 Array[vpy, {nt}]; fu = -T2 Cos[alpha] + T1 xp/R;(External force fu)
fv = -T2 Cos[alpha] V[[-1, All]]/l + T1 yp/R;(External force fv)
us = Sqrt[1 - (ds[[1]] . V)^2] - 1;(inextensibility constraint)
Do[uu[i, j] = 
    If[i == 1, 0, 
     h/2 Sum[(us[[k - 1, j]] + us[[k, j]]), {k, 2, i}]];, {i, nn}, {j,
    nt}];(u[t,s]= Integrate[us,{x,0,s}] )
Do[ll0[j] = fu[[j]]/(1 + us[[-1, j]]);, {j, nt}];
Do[ll[i, j] = 
    If[i == 1, 
     ll0[j], (ll0[j] + 
        h/2 ( Sum[[Mu] (uu[k, j] + uu[k, j - 2] - 2 uu[k, j - 1])/
               dt^2 + c/dt /2 (uu[k, j] - uu[k, j - 2]), {k, 1, 
             i - 1}] + 
           Sum[[Mu] (uu[k, j] + uu[k, j - 2] - 2 uu[k, j - 1])/dt^2 +
              c/dt /2 (uu[k, j] - uu[k, j - 2]), {k, 2, i}]))/(1 + 
        us[[i, j]])];, {i, nn}, {j, 3, nt}];
(the Lagrange multiplier 

[Lambda](t,s)=[Lambda]0(t)+Integrate[[Mu] D[u[t,x],t,t]+c 

D[u[t,x],t],{x,s,l}]/(1+D[u[t,s],s]))
bcrhs[j_] := (1 + 1/2 (ds[[1]] . V[[All, j]])^2) (ds[[2]] . 
      V[[All, j]])^2 + 
   ds[[2]] . 
     V[[All, j]] (2 ds[[1]] . V[[All, j]] ds[[2]] . V[[All, j]] + 
      4 (ds[[1]] . V[[All, j]])^3 ds[[2]] . 
        V[[All, j]]) + (1 + (ds[[1]] . V[[All, j]])^2 + (ds[[1]] . 
        V[[All, j]])^4) ds[[3]] . V[[All, j]];
(Initial Condition){x0, vx0, y0, vy0} = {.0, .01, 0, 
  0.05}; z0 = -Sqrt[R^2 - x0^2 - y0^2];
Do[uu[i, 1] = 0; uu[i, 2] = 0; vv[i, 1] = 0; 
 vv[i, 2] = 0;, {i, nn}]; Do[xx[i] = x0; vpx[i] = vx0; yy[i] = y0; 
 vpy[i] = vy0; zz[i] = z0; tt1[i] = -mp g R/z0; 
 tt2[i] = mp g/Sin[alpha], {i, 2}]; ll0[1] = -tt2[1] Cos[alpha]; 
ll0[2] = -tt2[2] Cos[alpha]; Do[ll[i, j] = ll0[1], {i, nn}, {j, 2}];
test = Table[.1, {nn}];
Do[(Verlet explicit step)
  fx = If[j <= 2, 0, 
    mp (U[[-1, j]] + U[[-1, j - 2]] - 2 U[[-1, j - 1]])/dt^2 + 
     cp (U[[-1, j]] - U[[-1, j - 1]])/dt ]; 
  fy = If[j <= 2, 0, 
    mp (V[[-1, j]] + V[[-1, j - 2]] - 2 V[[-1, j - 1]])/dt^2 + 
     cp (V[[-1, j]] - V[[-1, j - 1]])/dt ];
  xx[j + 1] = 
   xx[j] + vpx[j] dt - (fx + cp vpx[j] + tt1[j] xx[j]/R) dt^2/2 ; 
  vpx[j + 1] = vpx[j] - (fx + cp vpx[j] + tt1[j] xx[j]/R) dt; 
  yy[j + 1] = 
   yy[j] + vpy[j] dt - (fy + cp vpy[j] + tt1[j] yy[j]/R) dt^2/2 ; 
  vpy[j + 1] = vpy[j] - (fy + cp vpy[j] + tt1[j] yy[j]/R) dt;
  zz[j + 1] = -Sqrt[R^2 - xx[j + 1]^2 - yy[j + 1]^2]; 
  tt1[j + 1] = -R/
     zz[j + 1] (mp g + (mp (zz[j + 1] + zz[j - 1] - 2 zz[j])/dt^2 + 
        cp /dt/2 (zz[j + 1] - zz[j - 1])));
  tt2[j + 1] = -tt1[j + 1] zz[j + 1]/R/ Sin[alpha];
  (beam implicit step)
  r2 = EI ds[[1]] . bcrhs[j + 1] - 
    lambda[[All, j + 1]] (ds[[2]] . V[[All, j + 1]]);
  eq2 = [Mu] (V[[All, j + 1]] + V[[All, j - 1]] - 2 V[[All, j]]) + 
    c dt/2 (V[[All, j + 1]] - V[[All, j - 1]]) + dt^2 r2;
  eqs = Table[Drop[Drop[eq2, 2], -2][[i]] == 0, {i, nn - 4}]; 
  varAll = V[[All, j + 1]]; 
  bC0 = {(ds[[1]] . V[[All, j + 1]])[[1]] == 0, V[[1, j + 1]] == 0}; 
  bC1 = {lambda[[-1, j + 1]] (ds[[1]] . V[[All, j + 1]])[[-1]] - 
      EI bcrhs[j + 1][[-1]] == 
     fv[[j + 1]], (ds[[2]] . V[[All, j + 1]])[[-1]] == 0}; 
  eqAll = Join[eqs, bC0, bC1]; 
  ini = Table[{varAll[[i]], test[[i]]}, {i, Length[varAll]}]; 
  sol = Quiet@
    FindRoot[eqAll, ini, 
     Method -> {"Newton", "StepControl" -> "TrustRegion"}, 
     MaxIterations -> 20]; test = varAll /. sol; 
  Do[vv[i, j + 1] = test[[i]], {i, nn}];, {j, 2, 
   jmax - 1}] // AbsoluteTiming 

It takes about 1210 s on my laptop, finally we have similar pictures as above
Visualization $\lambda(t,s)$ (solid lines computed at s=sgrid) together with $\lambda_0(t)$ from Update 1 (red dashed line)