Integrating a function over a region defined as the epsilon-neighborhood of a triangle

Question

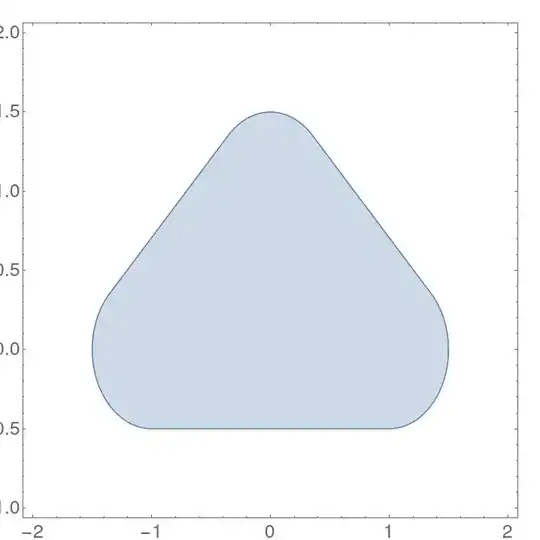
I would like to integrate the function f(x,y) = x^2 + y^2 over the epsilon-neighborhood of the triangle {{-1, 0}, {0, 1}, {1, 0}}. By epsilon-neighborhood, I mean the set of points which are closer to the triangle than epsilon (let's say epsilon = 0.5).

I do not know what is the best way to define such a region, how to plot it and how to integrate a function over it. I have tried the following code, but it gives back the incorrect result 0.3 even for the area (I don't know why). It seems that the same code works correctly for a Rectangle[{-1, -1}, {1, 1}], somehow.

RegT = Region[Triangle[{{-1, 0}, {0, 1}, {1, 0}}]]
(* Define the epsilon-neighborhood of a triangle *)
epsilon=0.5;
RegTneigh = ImplicitRegion[Norm[RegionNearest[RegT, {x, y}] - {x, y}, 2] <= epsilon, {x, y}]
(* Plotting the region (I don't know how to simply plot RegTneigh) *)
RegionPlot[Norm[RegionNearest[RegT, {x, y}] - {x, y}, 2] <= 0.5, {x, -2, 2}, {y, -1, 2}, ImagePadding -> 30, PlotPoints -> 30]
(* Checking the area of the region using f(x,y) = 1 *)

NIntegrate[1, {x, y} [Element] RegTneigh]

Answer 1

For Mathematica versions <13 try

eps=0.5
dreieck = Triangle[{{-1, 0}, {1, 0}, {0, 1}}]
\[CapitalDelta]eps =ImplicitRegion[RegionDistance[dreieck, {x, y}] <= eps, {x, y}]
Area[[CapitalDelta]eps] (4.19961)
NIntegrate[1,Element[{x,y},[CapitalDelta]eps]] (4.19961)
NIntegrate[x^2+y^2,Element[{x,y},[CapitalDelta]eps]] (3.5966)

Answer 2

• Here we even does not depend on RegionDistance or RegionNearest,see my privious answer. https://mathematica.stackexchange.com/a/244568/72111
• a point {x,y} belong to such dilation region iff there exists {p, q} ∈ triangle and {u, v} ∈ disk such that {x, y} == {p, q} + {u, v}

Clear["Global`*"];
epsilon=1/2;
disk = Disk[{0, 0},epsilon];
triangle = Triangle[{{-1, 0}, {0, 1}, {1, 0}}];
sol = Resolve[
   Exists[{p, q, u, 
     v}, {p, q} ∈ triangle && {u, v} ∈ disk, {x, 
      y} == {p, q} + {u, v}], Reals];
reg = ImplicitRegion[sol, {x, y}];
RegionPlot[reg, AspectRatio -> Automatic, 
 Epilog -> {Green, triangle}]
reg // Area
Integrate[1, {x, y} ∈ reg]
Integrate[x^2+y^2, {x, y} ∈ reg]

1/4 (8 + 4 Sqrt[2] + π)

1/4 (8 + 4 Sqrt[2] + π)

1/96 (136 + 88 Sqrt[2] + 27 π)

Answer 3

The magic word you are searching is: "RegionDilation". With this, your calculation looks like:

epsilon = 0.5;
region = 
  RegionDilation[Triangle[{{-1, 0}, {0, 1}, {1, 0}}], epsilon];
RegionPlot[region]
(Checking the area of the region using f(x,y)=1)
NIntegrate[1, {x, y} [Element] region]
(Doing the integral of f[x,y])
f[x_, y_] = x^2 + y^2;
NIntegrate[f[x, y], {x, y} [Element] region]