1

I have the following problem which I do not even know if there is a solution.

Say I have following integral:

Integrate[Sum[ToExpression["a" <> ToString@i] ChebyshevT[i, (2 t/tf - 1)], {i, 
0, 20}]*Sum[ ToExpression["b" <> ToString@i] ChebyshevT[i, (2 t/tf - 1)], {i, 0,
 20}] E^(a t), t]

$\int (\sum_{i=0}^{20}a_i T_i(t))(\sum_{i=0}^{20}b_i T_i(t))e^{at}dt$

Clearly, this integral is solvable and very easy. However, there are many terms, i.e. it is 400 very easy integrals. Mathematica struggles to execute the code in a reasonable time.

This is puzzling though, since any one of the integral is done quickly and 400 of them should naively be done in 400 the time. This is not the case.

Is it possible to handle such integrals (without doing any substantial amount of work per hand)? Mathematica does not allow for parallelization of sums of integrals, which is a bit weird.

I should mention that in the actual problem, the Chebyshevs are shifted and scaled, which makes it totally impossible to evaluate

Confuse-ray30
  • 347
  • 9

1 Answers1

1

one work around is

sum = Sum[a[i]*ChebyshevT[i, (2  t/tf - 1)], {i, 0, 20}]*
   Sum[b[i]*ChebyshevT[i, (2  t/tf - 1)], {i, 0, 20}]  E^(a  t);
Map[Integrate[#, t] &, Expand[sum]]

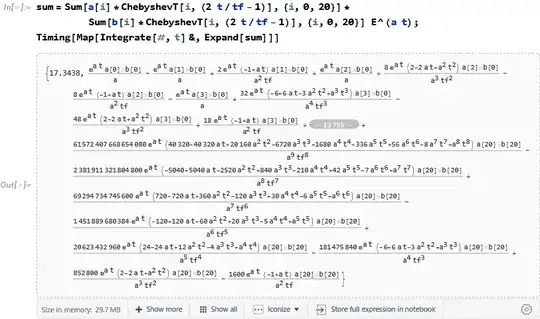
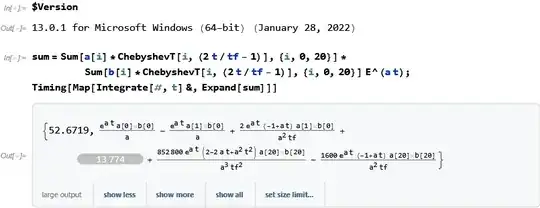
Mathematica graphics

took few seconds on my PC using V 14

Btw, the above is also much faster than using Distribute

Distribute[Integrate[Expand[sum], t]]]

Update

In V 14 took 17 seconds

Mathematica graphics

In V 13 took 52 seconds. All on same PC

Mathematica graphics

I read that V 14 has lots of performance improvements.

Can someone provide an explanation as to why Map is so much faster than just Integrate?

I think this might give clue. See help in Integrate under possible issues. It says

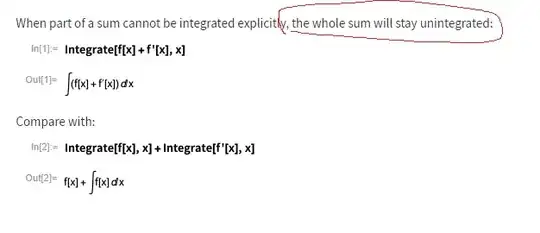
enter image description here

The above implies that Mathematica does not automatically distribute Integrate over sum. So use has to do this themselfs. One way is using Map.

Nasser
  • 143,286
  • 11
  • 154
  • 359
  • Can you test it on v13 as well? My Mathematica takes about a minute (which is still a huge improvement). Also can you elaborate as to why it is so much faster? Does Mathematica not Expand the polynomials if you do not tell it to when doing Integrate? – Confuse-ray30 Jan 18 '24 at 12:24
  • @Confuse-ray30 added timing. V 14 is 17 seconds, V 13 is 52 seconds. I think you need to do expand. I do not think Integrate itself will do that. – Nasser Jan 18 '24 at 12:32
  • @Confuse-ray30 actually if you do not do Expand, it is faster. Try and see which one you want to use. Both in V 13 and V 14 they finish much faster using Map, but without Expand. – Nasser Jan 18 '24 at 12:37
  • If someone else reads this: Can someone provide an explanation as to why Map is so much faster than just Integrate? – Confuse-ray30 Jan 18 '24 at 12:50
  • Thanks, your method is indeed a lot faster. Now Im wondering why though. – Confuse-ray30 Jan 18 '24 at 12:52
  • @Confuse-ray30 added a note about why Map sometimes is needed. But this issue was raised in this forum before actually. see this question which is similar to yours – Nasser Jan 18 '24 at 12:59
  • Map with Extend@sum and without Extend does not seem to give me the same expression. (I tested it for 3 Chebyshevs rather than 20 and compared the coefficients for t) – Confuse-ray30 Jan 18 '24 at 14:33
  • No, your method does not work: Map[Integrate[#, t] &, t] gives t. I think Mathematica never integrated anything in the first place, which is why this is so quick. Distribute works however. – Confuse-ray30 Jan 18 '24 at 14:54
  • 1
    @Confuse-ray30 map works but you are not using it correct. Try Map[Integrate[#,t]&,t+1] gives t+t^2/2. On a single item it has to be a list, like this Map[Integrate[#,t]&,{t}] gives {t^2/2}. You can't map on atomic item. You said your input is a sum. You can always write a wrapper function to handle the special case. – Nasser Jan 18 '24 at 16:15