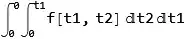Symbolic multiple Integrals not delivering expected zero result

Question

Consider the following function defined as a double-integral:

$ int_{2D}(h)=\int_0^h \int_0^{t_1}f(t_1,t_2) dt_2 dt_1 $.

Clearly, $int_{2D}(0)=0$ as long as $f(t_1,t_2)$ is well-behaved.

The previous function can be easily translated into Mathematica's language

int2d[h_]:=Integrate[f[t1,t2],{t1,0,h},{t2,0,t1}]

Now, evaluate

int2d[0]

to obtain the output

\!\( \*SubsuperscriptBox[\(\[Integral]\), \(0\), \(0\)]\( \*SubsuperscriptBox[\(\[Integral]\), \(0\), \(t1\)]f[t1, t2] \[DifferentialD]t2 \[DifferentialD]t1\)\)

The previous expression suggests that Mathematica is giving the literal result, namely

$ int_{2D}(0)=\int_0^0 \int_0^{t_1}f(t_1,t_2) dt_2 dt_1 $

Is there any way that Mathematica provides a vanishing result (as it should be)? Is it necessary to define rules in the spirit of https://mathematica.stackexchange.com/a/38171/90163 ?

(I found one way to solve it, but I would like to avoid the approach that I am presenting below. By a simple change of variables rewrite $int_{2D}$ as

$int_{2D}(h)=h^2\int_0^1 \int_0^{1}f(hs_1,hs_1 s_2) ds_2 ds_1 $,

and then translate the above expression into Mathematica)

This situation contrasts with the one-dimensional case, where one defines

int1D[h_]=Integrate[f[t1],{t1,0,h}]

Thus, evaluating int1D(0) one obtains 0.

Answer 1

In Mathematica, the command

Integrate[g[x, y], {x, 0, a}, {y, 0, b}]

Is as if one wrote

$$ \int_{0}^{a}\left( \int_{0}^{b}g\left( x,y\right) dy\right) dx $$

And not

$$ \int_{0}^{b}\left( \int_{0}^{a}g\left( x,y\right) dx\right) dy $$

Notice the order. i.e The inner limit $\{x,0,a\}$ in the command is used on the outer integral and the outer limit in the command $\{y,0,b\}$ is used on the inner integral.

This is confusing but known. There are number of posts on this in this forum if you search.

Because of this, your call to int2d gives

int2d[h_] := Integrate[f[t1, t2], {t1, 0, h}, {t2, 0, t1}]
int2d[0]

And because the inner integral does not evaluate the whole thing remains unevaluated. You can fix this if you change the order as mentioned in comment.

But the easy solution is to use explicit Integrate command for each. Now you decide on the order explicitly. Like this

intV1[h_] := Integrate[Integrate[f[t1, t2], {t2, 0, t1}], {t1, 0, h}]
intV2[h_] := Integrate[Integrate[f[t1, t2], {t1, 0, h}], {t2, 0, t1}]

Both now will give zero

intV1[0]
intV2[0]

see

Why does Mathematica list the variables in a double integral backwards?

Order of integration changes output of indefinite multiple integral in Mathematica 7

How to convert Integrate[Integrate[...] ...] into multiple integral