Get interior of mesh region

Question

I really like the functionality of Mathematica for mesh-based regions,
and have enough understanding of it. But this problem bothers me.
There is a similar question, but the functionality used now obsolete.

Let we have mesh region (for simplicity MeshCellMeasure made large enough):

region = DiscretizeRegion[Annulus[{0, 0}, {1/2, 1}, {0,3 Pi/2}], {MaxCellMeasure -> {"Length" -> 0.15}, ImageSize -> 150}]

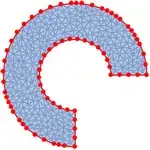
I need to separate the interior — all that is not RegionBoundary@region.
And in the form in which it is obtained at primary discretization;
literally everything that is not highlighted red:

bound = RegionBoundary@region;
Show[region, 
 HighlightMesh[
  bound, {Style[1, Red], Style[0, PointSize[Medium], Red]}]]

I was only able to do it this way:

coords = MeshCoordinates@region;
boundCoords = MeshCoordinates@bound;
verts = Range@Length@coords;
boundVerts = Flatten[Position[coords, #] & /@ boundCoords, 2];
interior = 
 ConcaveHullMesh[coords[[Delete[verts, Partition[boundVerts, 1]]]]]

In fact, it is simplest form of erosion, but I can't get it nor with RegionErosion nor with Erosion.

I’m sure it can be made simpler and more contemporary,
thanks for help in advice!

@user64494, it makes solid region without mesh. I need to preserve mesh from initial region! — lesobrod, Jan 19 '24 at 17:08
@lesobrod The "interior" is the remaining mesh when all boundary lines are removed? — Ulrich Neumann, Jan 19 '24 at 17:45

kglr · Accepted Answer · 2024-01-19T23:16:51.070

8

interior = {interiorpoints, interiorlines, interiorpolygons} = 
   MeshCells[region, {#, "Interior"}] & /@ {0, 1, 2};

HighlightMesh[region, interior, ImageSize -> Large]

Row[HighlightMesh[region, ToExpression@#, 
   ImageSize -> Medium, PlotLabel -> Style[#, 20]] & /@ 
 {"interiorpoints", "interiorlines", "interiorpolygons"}]

Graphics[{EdgeForm[Gray], RandomColor[], #} & /@ 
   MeshPrimitives[region, {2, "Interior"}]]

edited Jan 19 '24 at 23:16

answered Jan 19 '24 at 20:35

kglr

394,356
18
477
896

1

Very interesting answer ! Where did you find the option "Interior"? Options[MeshCells] gives {}! Thanks – Ulrich Neumann Jan 20 '24 at 09:44
1

@UlrichNeumann, afaik these syntaxes/properties are not documented. I don't remember how I bumped into things like {1,"Interior"} , {2, "Frontier"} , {0,"Boundary"} as valid cell indices. (I played with the list returned by mesh["Properties"] (where mesh is a MeshRegion or a BoundaryMeshRegion object) and found some properties can be accessed using these propery names.) related: Boundary cells of a mesh?, total length of edges in select Voronoi diagram – kglr Jan 20 '24 at 10:06
Thanks for YouTube helpfull Auswertung! – Ulrich Neumann Jan 20 '24 at 11:10
1

@kglr, OMG, I play sometimes with "Properties", but there are lot of non documented for MeshRegion... Even "DeepCopy" (o_O)
Thank you anyway, that works for version 12, 13 and 14 very well! – lesobrod Jan 20 '24 at 14:39

Greg Hurst · Answer 2 · 2024-01-22T15:37:28.290

Here's a way to remove only the faces that have an edge on the boundary. This differs from MeshCells[region, {2, "Interior"}] since that also excludes faces with only a point touching the boundary.

g = MeshConnectivityGraph[region, {1, 2}, 1];
bdedges = Pick[VertexList[g], VertexDegree[g], 1];
bdfaces = VertexOutComponent[g, bdedges, {1}][[All, 2]];
interiorfaces = Complement[Range[MeshCellCount[region, 2]], bdfaces];
submesh = MeshRegion[
  MeshCoordinates[region], 
  MeshCells[region, {2, interiorfaces}]
]

HighlightMesh[region, {2, interiorfaces}]

Get interior of mesh region

2 Answers2