This is interesting example. All replacements after FullSimplify are not applied. That is why.
Lets look at very simple example to better see this.
ClearAll["Global`*"]
expr = (n - k) + m;
expr /. {(n - k) :> b} // Simplify /. m :> e
The above says to replace (n - k) by b, which will give b+m and then to replace m by e which should result in b+e. But it does not. It results in b+m. The whole thing after // Simplify is simply not used (Trace confirms this).

You can either do one of the following two options. The first as suggested by xzczd in comment above
ClearAll["Global`*"]
expr = (n - k) + m;
(expr /. {(n - k) :> b} // Simplify) /. m :> e

Or move // Simplify to the very end!
ClearAll["Global`*"]
expr=(n-k)+m;
expr/.{(n-k):> b}/.m:>e//Simplify
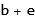
Basically, adding //Simplify in the middle has the effect of short circuiting the computation. So rule of thumb, always add // at very end of the command and not in the middle. (I never add // command in middle of commands myself because I simply do not like to chain too many commands into one long one and prefer to write many smaller commands one after the other). The code might becomes longer but for me it is more clear.
To see this, just do Trace and you will see that everything after //Simplify is not applied.




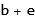

(f[n, k, x] /. {(n - k) :> \[Beta] - 1, k :> \[Alpha]} // FullSimplify) /. (1 + n) :> \[Alpha] + \[Beta]When you're not sure about precedence, try N-click the code, or press Ctrl + . to check the precedence: https://mathematica.stackexchange.com/a/249596/1871 – xzczd Jan 21 '24 at 04:30