2

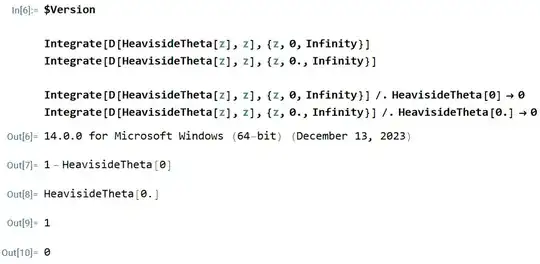
As the following figure described, why does HeavisideTheta give different value at the point 0 and 0.? Especially at the coordinate origin, one gives the value 1 and another 0 when HeavisideTheta[0]=0. Isn't 0 and 0. the same point?

Note: DiracDelta gives similar result at 0 and 0. as the following figure.

Thanks!

$Version

Integrate[D[HeavisideTheta[z], z], {z, 0, Infinity}]
Integrate[D[HeavisideTheta[z], z], {z, 0., Infinity}]


Integrate[D[HeavisideTheta[z], z], {z, 0, Infinity}] /. 
 HeavisideTheta[0] -> 0
Integrate[D[HeavisideTheta[z], z], {z, 0., Infinity}] /. 
 HeavisideTheta[0.] -> 0

enter image description here

enter image description here

likehust
  • 693
  • 3
  • 8
  • Note that Integrate[DiracDelta[z], {z, 0, Infinity}] and Integrate[DiracDelta[z], {z, 0., Infinity}] give the same results. So it might be that this behavior is a consequence of how DiracDelta handles exact vs. numerical inputs. – Michael Seifert Jan 23 '24 at 14:30
  • HeavisideTheta is an implementation of the antiderivative of $\delta$-distribution in Mathematica. This is a distribution too and the integral Integrate[D[HeavisideTheta[z], z], {z, 0, Infinity}] makes no sense in traditional math (e.g, see Wiki for info). HeavisideTheta[0] is an invetion of Mathematica developers, not a math notion. – user64494 Jan 23 '24 at 14:39
  • @Michael Seifert, Thanks. A description has been added based on your comments. – likehust Jan 23 '24 at 14:40
  • @user64494, Thanks. Why Heaviside gives different values at the point 0 at the website? – likehust Jan 23 '24 at 14:45
  • @likehust: As the documentation says "Numerical routines will typically miss the contributions from measures at single points:" and gives an (incorrect) example NIntegrate[DiracDelta[x], {x, -2, 1}]. As I know it, most of applications of distributions lie in ODEs and PDEs and don't require any integration. – user64494 Jan 23 '24 at 14:53
  • @user64494: The documentation says "H(0) = 0 is used when H needs to be left-continuous. In this case H is an indicator function of an open semi-infinite interval", this is just I want. I can not figure out they how to use the value. Thank you. – likehust Jan 23 '24 at 15:00
  • Concerning the liked by you Wiki page, "This page was last edited on 1 November 2023, at 09:13 (UTC)" . This page is often edited and its references are not solid. – user64494 Jan 23 '24 at 15:01
  • @likehust: I repeat the support of HeavisideTheta is 0 and HeavisideTheta[0] makes no sense. The developers wrongly change HeavisideTheta by a usual function UnitStep. That's all. – user64494 Jan 23 '24 at 15:04
  • @user64494, Thanks, You are an authority in this field. Plus, can you help me study the method about the heaviside in the article, Thank you very much. – likehust Jan 23 '24 at 15:10
  • @likehust: You wrote "Plus, can you help me study the method about the heaviside in the article". Unfortunately, I am not a specialist in this field. – user64494 Jan 23 '24 at 16:21
  • 1
    I'd say it's just the current design of HeavisideTheta. Probably there won't be a simple solution like setting an option or turning to another built-in function (you're looking for something like this, right?) I believe the easiest solution is coding a function that behaves as expected all by oneself (as I've done under this question of yours ). – xzczd Jan 24 '24 at 03:08
  • @xzczd, Thank you very much. You are right. I will use a user-defined function to deal with the real problem based on your suggestion in the future. Thanks again. – likehust Jan 24 '24 at 14:29

0 Answers0