Obtain/extract PlotRange values from a ListPlot

Question

Note: I'm running Mathematica 9.0, which is quite an old version. But I'd like potential answers to be applicable to Mathematica 9.0, if possible.

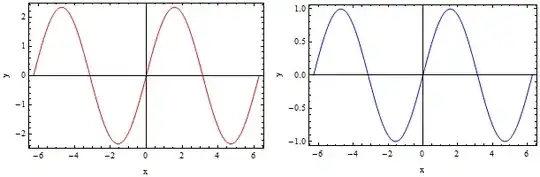
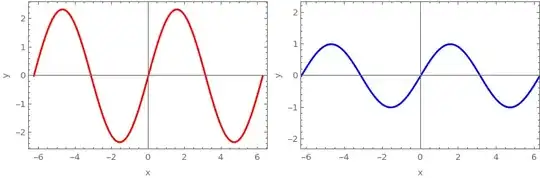
In the following example, I have two ListPlot objects, myPlot1 and myPlot2. Each has PlotRange -> All to show all of the points.

How can I extract the PlotRange parameters from myPlot1? My goal is to give myPlot2 the same PlotRange parameters as myPlot1 without knowing those parameters a priori.

myPts1 = Table[{x, 2.333*Sin[x]}, {x, -2 Pi, 2 Pi, 2 Pi/50}];
myPts2 = Table[{x, Sin[x]}, {x, -2 Pi, 2 Pi, 2 Pi/50}];
imageSize = 300;
myPlot1 = 
  ListPlot[myPts1, PlotRange -> All, Joined -> True, Frame -> True, 
   FrameLabel -> {"x", "y"}, PlotStyle -> Red, ImageSize -> imageSize];
myPlot2 = 
  ListPlot[myPts2, PlotRange -> All, Joined -> True, Frame -> True, 
   FrameLabel -> {"x", "y"}, PlotStyle -> Blue, 
   ImageSize -> imageSize];
Grid[{{
   myPlot1, myPlot2
   }}]

You can use the GraphicsInformation functionality, either here in versions before ResourceFunction is available, or here if ResourceFunction works. — Carl Woll, Feb 07 '24 at 20:30

score 3 · Accepted Answer · answered Feb 07 '24 at 18:57

myPts1 = Table[{x, 2.333*Sin[x]}, {x, -2 Pi, 2 Pi, 2 Pi/50}];

imageSize = 300;

myPlot1 =
 ListPlot[myPts1, PlotRange -> All, Joined -> True, Frame -> True, 
  FrameLabel -> {"x", "y"}, PlotStyle -> Red, ImageSize -> imageSize]

Now use AbsoluteOptions:

AbsoluteOptions[myPlot1, PlotRange]

{PlotRange -> {{-6.28319, 6.28319}, {-2.3284, 2.3284}}}

score 2 · Answer 2 · answered Feb 07 '24 at 18:59

Options[myPlot1] gives you the information you're looking for:

Options[myPlot1]
(*{DisplayFunction -&gt; Identity, DisplayFunction -&gt; Identity, 

AspectRatio -> 1/GoldenRatio, Axes -> {True, True}, 
 AxesLabel -> {None, None}, AxesOrigin -> {0, 0}, 
 DisplayFunction :> Identity, Frame -> {{True, True}, {True, True}}, 
 FrameLabel -> {{"y", None}, {"x", None}}, 
 FrameTicks -> {{Automatic, Automatic}, {Automatic, Automatic}}, 
 GridLines -> {None, None}, GridLinesStyle -> Directive[
GrayLevel[0.5, 0.4]], ImageSize -> 300, 
 Method -> {"OptimizePlotMarkers" -> True, 
   "OptimizePlotMarkers" -> True, 
   "CoordinatesToolOptions" -> {"DisplayFunction" -> ({Identity[#1[[
           1]]], Identity[#1[[2]]]} &), 
     "CopiedValueFunction" -> ({Identity[#1[[1]]], 
         Identity[#1[[2]]]} &)}}, 
 PlotRange -> {{-6.28319, 6.28319}, {-2.3284, 2.3284}}, 
 PlotRangeClipping -> True, 
 PlotRangePadding -> {{Scaled[0.02], Scaled[0.02]}, {Scaled[0.05], 
    Scaled[0.05]}}, Ticks -> {Automatic, Automatic}}*)

Unfortunately, on the version of Mathematica I'm using, Options[myPlot1] gives me only (*{FrameLabel -> {"x", "y"}, AspectRatio -> 1/GoldenRatio, Axes -> True, AxesOrigin -> {0., 0.}, Frame -> True, FrameLabel -> {"x", "y"}, ImageSize -> 300, Method -> {}, PlotRangeClipping -> True}*). PlotRange is not listed. Do you have any ideas about how I can obtain the PlotRange values in Mathematica 9.0? — Andrew, Feb 07 '24 at 19:20
UPDATE: AbsoluteOptions[myPlot, PlotRange] does the trick on Mathematica 9.0, giving the output (* {PlotRange -> {{-6.28319, 6.28319}, {-2.3284, 2.3284}}} *). — Andrew, Feb 07 '24 at 19:24

score 2 · Answer 3 · answered Feb 07 '24 at 19:00

myPts1 = Table[{x, 2.333*Sin[x]}, {x, -2 Pi, 2 Pi, 2 Pi/50}];
myPts2 = Table[{x, Sin[x]}, {x, -2 Pi, 2 Pi, 2 Pi/50}];
imageSize = 300;
myPlot1 = 
  ListPlot[myPts1, PlotRange -> All, Joined -> True, Frame -> True, 
   FrameLabel -> {"x", "y"}, PlotStyle -> Red, 
   ImageSize -> imageSize];

pr1 = AbsoluteOptions[myPlot1, PlotRange]

myPlot2 = 
  ListPlot[myPts2, pr1, Joined -> True, Frame -> True, 
   FrameLabel -> {"x", "y"}, PlotStyle -> Blue, 
   ImageSize -> imageSize];
Grid[{{myPlot1, myPlot2}}]

kglr · Answer 4 · 2024-02-08T00:09:05.280

Update: Using ResourceFunction["GraphicsInformation"] we get a plot range taking into account the PlotRangePadding setting of the input graphics:

graphicsInfo = ResourceFunction["GraphicsInformation"];
graphicsInfo[myPlot1] // Column

plotrange = "PlotRange" /. graphicsInfo[myPlot1]

{{-6.54498, 6.54498}, {-2.58711, 2.58711}}

myPlot2 = 
  ListPlot[myPts2, 
   PlotRange -> plotrange, 
   Joined -> True, Frame -> True, FrameLabel -> {"x", "y"}, 
   PlotStyle -> Blue, ImageSize -> imageSize];
Grid[{{myPlot1, myPlot2}}]

Original answer:

PlotRange[myPlot1]

{{-6.28319, 6.28319}, {-2.3284, 2.3284}}

Just use PlotRange[myPlot1] instead of All as option setting in myPlot2:

myPlot2 = 
  ListPlot[myPts2, 
   PlotRange -> PlotRange[myPlot1], 
   Joined -> True, 
   Frame -> True, 
   FrameLabel -> {"x", "y"}, 
   PlotStyle -> Blue, 
   ImageSize -> imageSize];
Grid[{{myPlot1, myPlot2}}]

Note: Afaik, this usage of PlotRange as a function to extract the option setting does not appear in documentation.

Notice that myPlot1 uses PlotRangePadding, so you either need to include it explicitly in myPlot2 or you need to compute what the PlotRange would be with the added padding. Otherwise, as you can see in your plots, the plot range of myPlot2 is slightly smaller than myPlot1. — Carl Woll, Feb 07 '24 at 20:33
Thank you @CarlWoll, excellent point. I updated with a fix using your "GraphicsInformation". — kglr, Feb 07 '24 at 21:59

Obtain/extract PlotRange values from a ListPlot

4 Answers4