0

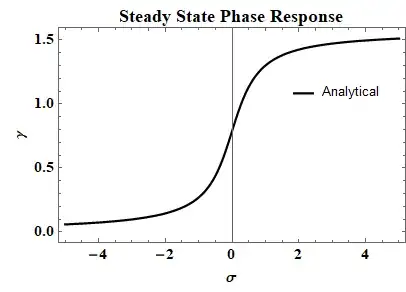
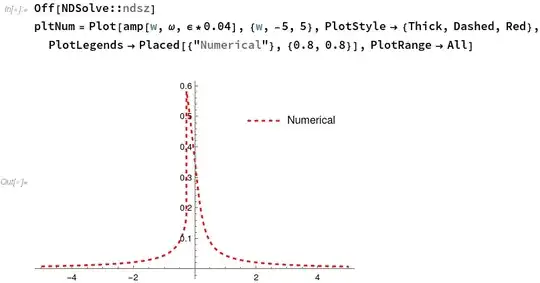
I have a code to plot the steady state frequency response curve (provided by @ Michael E2), How can I plot the steady state phase response with the help of this code same as shown in the figure:

Steady state phase response obtained analytically.

\[Kappa]=1.4;
WE = 0.2;
\[Omega] = Sqrt[3*\[Kappa]*(1 + WE) - WE];
f = 0.2;
\[Epsilon] = 0.2;

amp[w_, w0_?NumericQ, damping_?NumericQ] /; w == 0 = 1.;
amp[w_?NumericQ, w0_?NumericQ, damping_?NumericQ] := 
  Block[{x}, #[#["Domain"][[1, -1]]] &[
    x /. First@
      NDSolve[{x''[
          T] == (1/[Epsilon])((((1 + 
                 WE)(1 + [Epsilon]x[T])^(-3[Kappa] - 
                  1))) - ((1 + [Epsilon]*
                 x[T])^-1) - (WE(1 + [Epsilon]x[T])^-2) - (4*
              damping[Epsilon]^2(x'[
                T])(1 + ([Epsilon]
                   x[T]))^-2) - ((3[Epsilon]^2(x'[
                   T]^2)(1 + [Epsilon]x[T])^-1)/2) - [Epsilon]^3*
             fSin[T (w0 + [Epsilon]^2 w)]), x[0] == 1, x'[0] == 0, 
        WhenEvent[x'[T] < 0 && T > 5000, "StopIntegration"]}, 
       x, {T, 0, 5010}]]];
 Off[NDSolve::ndsz]
pltNum = Plot[
  Evaluate[Table[
    amp[w, [Omega], z], {z, {[Epsilon]*0.04}}]], {w, -5, 5}, 
  PlotStyle -> {Thick, Dashed, Red}, 
  PlotLegends -> Placed[{"Numerical"}, {0.8, 0.8}], PlotRange -> All]

Any help would be highly appreciated. Thanks!

user64494
  • 26,149
  • 4
  • 27
  • 56
Abhishek
  • 81
  • 5

1 Answers1

0

Is this what you want?

The provided graph and the variables in the code are different. It is difficult to know what exactly you want to plot here.

enter image description here

If possible please share the link where you get the graph or the code. just sharing the author's name is not enough.

user444
  • 2,414
  • 1
  • 7
  • 28
  • Thanks for the reply. The plot you have shown here is correct (which I am getting from the code), but it is steady state amplitude vs frequency. I just want to plot steady state phase response. Is there any way (modification) that I could use the above code to plot the phase response curve. – Abhishek Feb 08 '24 at 07:32
  • I am sharing the link from where I got the code. – Abhishek Feb 08 '24 at 07:59