Numerical Solution for a Non-Linear Functional Fractional Differential Equation (FFDE)

Question

I tried solve non-linear Functional-Fractional Differential Equation (FFDE) with this method, but it works on only for range: $x\in \{0,1\}$.

I what extend the solution range for example for general a and b.

a =-3;
b = 2;
DSolve[{CaputoD[y[x], {x, 3/2}] - Sqrt[y[x]] - y[2 x- 1] == 0, y[x /; x <= 0] == 2, y'[x /; x <= 0] == 1}, y[x], {x, a, b}]

How to change the code to work for range $x\in \{-3,2\}$ and plot solution ?

Answer 1

This is fractional delayed differential equation (FDDE), therefore we can't use method described in my answer here. Instead of the Haar wavelets method we try to use implicit difference scheme described in this paper. Note that for this type of equations we need to define $y(x)$ at $x\le 0$ and at $2x-1\ge a$ as well. Without this data we can't compute an unique solution. While for $x\le 0$ we have $y(x)=2, y'(x)=0$ (it could not be y'(x)=1 as given above), for $2x-1\ge 2$ we have no data. So, we put for example $f(2 x-1)=0, 2 x-1\ge 2$. To reduce the Caputo derivative order we introduce a new variable $z=y'(x)$, then our code is follows

L = 2; dx = L/100; xgrid = Range[0, L, dx]; nn = Length[xgrid];
M1 = NDSolve`FiniteDifferenceDerivative[Derivative[1], xgrid, 
    DifferenceOrder -> 2]@"DifferentiationMatrix";
Z = Array[zz, {nn}]; Y = Array[yy, {nn}]; y0 = 2; dy0 = 0;
eq1 = Drop[Z - M1 . Y, 1]; bc = {Z[[1]] - dy0, Y[[1]] - y0};
a[j_][q_] := (j + 1)^(1 - q) - j^(1 - q);
b[j_][q_] := ((j + 1)^(2 - q) - j^(2 - q))/(2 - 
      q) - ((j + 1)^(1 - q) + j^(1 - q))/2;
eq2 = Table[0, {nn - 1}]; q = 1/2; Do[
 c[0] = If[n == 1, 1, a[0][q] + b[0][q]]; 
 If[n >= 2, 
  Do[c[j] = a[j][q] + b[j][q] - b[j - 1][q];, {j, 1, n - 2}]; 
  c[n - 1] = a[n - 1][q] - b[n - 2][q]]; 
 eq2[[n - 1]] = 
  dx^(-q)/Gamma[2 - q] (c[0] Z[[n]] - c[n - 1] Z[[1]] - 
      Sum[(c[n - j - 1] - c[n - j]) Z[[j]], {j, 1, n - 1}]) - 
   Sqrt[Y[[n]]] - 
   If[2 xgrid[[n]] - 1 <= 0, y0, 
    If[Round[(2 xgrid[[n]] - 1)/dx] >= nn + 1, 0, 
     Y[[Round[(2 xgrid[[n]] - 1)/dx]]]]];, {n, 2, nn}];
varALL = Join[Y, Z]; eqAll = Join[eq1, eq2, bc];
{res, {evx}} = 
  Reap[FindRoot[Table[eqAll[[i]] == 0, {i, Length[eqAll]}], 
    Table[{varALL[[i]], .1}, {i, Length[varALL]}], 
    Method -> {"Newton", "StepControl" -> "TrustRegion"}, 
    MaxIterations -> 1000, EvaluationMonitor :> Sow[varALL]]];

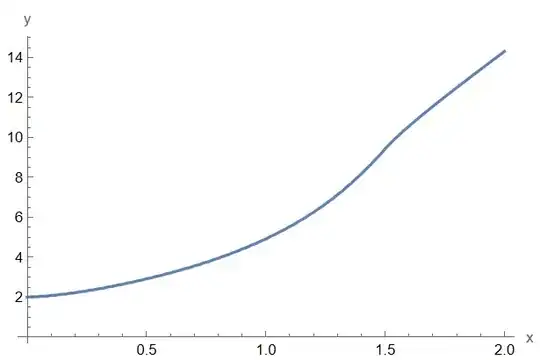
Visualization

ListLinePlot[Transpose[{xgrid, Y /. res}], AxesLabel -> {"x", "y"}]