How can I build a cycled curve from three orientable Bezier curves and fill the curved region?

Question

The desired result is

pts1 = {{0, 0}, {1, 1}, {2, -1}, {3, 0}, {5, 2}, {6, -1}, {7, 3}};
pts2 = {{5, -2}, {0, 0}, {1, 2}, {5, 1}, {2, 2}, {4, 3}, {5, 4}};
pts3 = {{4, 2}, {3, 2}, {2, 3}, {-1, -3}};
curves = {curve1, curve2, curve3} = 
   BezierCurve /@ {pts1, pts2, pts3};
Graphics[{Arrowheads[.02], Arrow /@ curves}]

Did you try BezierFunction? It allows making the curve in the desired range. — Rom38, Feb 15 '24 at 09:22

Ulrich Neumann · Answer 1 · 2024-02-15T10:53:50.107

First we need new definition of BezierFunction because actually (Mathematica v12.2) it's not possible to define Norm[BezierFunction[pts1][t]-pt] correctly

Find optimal BezierFunction (thanks @SjoerdSmid!)

bezCurve[{pt : {_, _}}] := pt &;
bezCurve[ctrlPts_?MatrixQ] := bezCurve[ctrlPts] = With[{
     b1 = bezCurve[Most[ctrlPts]],
     b2 = bezCurve[Rest[ctrlPts]]}(* 
    geometrische Konstruktion Bezierkurve*)
    , (1 - #)*b1[#] + #*b2[#] &];
(* hier wird erst der Kurvenparameter t eingeführt*)
bezCurve[ctrlPts_?MatrixQ, t_] := Simplify[bezCurve[ctrlPts][t]];

plot curves and find intersections

pts1 = {{0, 0}, {1, 1}, {2, -1}, {3, 0}, {5, 2}, {6, -1}, {7, 3}};
pts2 = {{5, -2}, {0, 0}, {1, 2}, {5, 1}, {2, 2}, {4, 3}, {5, 4}};
pts3 = {{4, 2}, {3, 2}, {2, 3}, {-1, -3}};
curves = {curve1, curve2, curve3} =Map[Function[u, Evaluate@bezCurve[#, u]] &, {pts1, pts2, pts3}];
bild = ParametricPlot[{curve1[u], curve2[u], curve3[u] }, {u, 0, 1},PlotStyle -> {Red, Green, Blue}];
sp = GraphicsMeshFindIntersections[bild[[All, 1]]  ]
(* intersection points {{0.856312, 0.241003}, {2.00301, 0.0857585},{3.25519, 2.06216}}*)
Show[bild, Graphics[Point[sp]]]

Now we find the parts of the beziercurves

{u11, u12} = {ArgMin[Norm[curve1[t] - sp[[1]]], t],ArgMin[Norm[curve1[t] - sp[[2]]], t]}
{u21, u22} = {ArgMin[Norm[curve2[t] - sp[[2]]], t],ArgMin[Norm[curve2[t] - sp[[3]]], t]}
{u31, u32} = {ArgMin[Norm[curve3[t] - sp[[1]]], t],ArgMin[Norm[curve3[t] - sp[[3]]], t]}
pic = Show[{ParametricPlot[curve1[u], {u, u11, u12}], 
ParametricPlot[curve2[u], {u, u21, u22}], 
ParametricPlot[curve3[u], {u, u31, u32}] } , PlotRange -> All] ;
Show[bild,Graphics[{FaceForm[Lighter[Gray]], EdgeForm[Black],
Polygon[Cases[pic, Line[p_] :> p, -1] // Flatten[#, 1] &]}]]

BezierCurve is different from BezierFunction , we can see that the curves and region is difference to the desired result. — herbertfederer, Feb 15 '24 at 22:16
@herbertfederer That is already clear . But BezierCurve is a Graphics primitive which doesn't allow access to plotted points . That's why I took BezierFunction in my answer! — Ulrich Neumann, Feb 16 '24 at 08:21
@herbertfederer If you really need piecewise cubic spline like BezierCurve you should redefine 4-point Bezierspline {(1 - u)^3, 3 u (1 - u)^2, 3 u^2 (1 - u), u^3} .{p1,p2,p3,p4} — Ulrich Neumann, Feb 16 '24 at 17:17

cvgmt · Answer 2 · 2024-02-22T11:53:59.200

Edit

Does not depend on PlanarFaceList and we can distinct the boundary lines.

Clear["Global`*"];
pts1 = {{0, 0}, {1, 1}, {2, -1}, {3, 0}, {5, 2}, {6, -1}, {7, 3}};
pts2 = {{5, -2}, {0, 0}, {1, 2}, {5, 1}, {2, 2}, {4, 3}, {5, 4}};
pts3 = {{4, 2}, {3, 2}, {2, 3}, {-1, -3}};
curves = {curve1, curve2, curve3} = 
   BezierCurve /@ {pts1, pts2, pts3};
g = Graphics[{Arrowheads[.02], Arrow /@ curves}];
lines = MeshPrimitives[DiscretizeGraphics@#, 1] & /@ curves;
data = RegionMeshSplitIntersectingSegments[lines];
pts = data[[1]];
splits = data[[2]];
intersections = Cases[splits, l_ /; Length@l == 3, -1];
boundaryLinesIndexs = 
  Join[{#[[1, 2]]}, Range[#[[1, -1]], #[[2, 1]]], {#[[2, 2]]}] & /@ 
   Partition[intersections, 2];
reg = BoundaryMeshRegion[pts, Line /@ boundaryLinesIndexs];
Graphics[{{HatchFilling[], reg}, curves, Arrowheads[{{Large, .5}}], 
  Thread[{{Red, Green, Blue}, 
    Arrow@pts[[#]] & /@ boundaryLinesIndexs}]}]

https://mathematica.stackexchange.com/a/295351/72111 still work for this case, but it can not distinct the three boundary lines.

Clear["Global`*"];
pts1 = {{0, 0}, {1, 1}, {2, -1}, {3, 0}, {5, 2}, {6, -1}, {7, 3}};
pts2 = {{5, -2}, {0, 0}, {1, 2}, {5, 1}, {2, 2}, {4, 3}, {5, 4}};
pts3 = {{4, 2}, {3, 2}, {2, 3}, {-1, -3}};
curves = {curve1, curve2, curve3} = 
   BezierCurve /@ {pts1, pts2, pts3};
g = Graphics[{Arrowheads[.02], Arrow /@ curves}];

lines = MeshPrimitives[DiscretizeGraphics@curves, 1];
data = Region`Mesh`SplitIntersectingSegments[lines];
pts = data[[1]];
splits = data[[2]];
segments = Flatten[Partition[#, 2, 1] & /@ splits, 1];
graph = Graph[Range@Length@pts, UndirectedEdge @@@ segments, 
   VertexCoordinates -> pts];
faces = PlanarFaceList[graph];
polys = Polygon[pts[[#]]] & /@ faces;
Show[g, Graphics[{HatchFilling[], EdgeForm[{Thick, Red}], 
   polys[[2]]}]]

From https://mathematica.stackexchange.com/a/275381/72111

Clear["Global`*"];
pts1 = {{0, 0}, {1, 1}, {2, -1}, {3, 0}, {5, 2}, {6, -1}, {7, 3}};
pts2 = {{5, -2}, {0, 0}, {1, 2}, {5, 1}, {2, 2}, {4, 3}, {5, 4}};
pts3 = {{4, 2}, {3, 2}, {2, 3}, {-1, -3}};
curves = {curve1, curve2, curve3} = 
   BezierCurve /@ {pts1, pts2, pts3};
reg = RegionUnion[DiscretizeGraphics /@ curves];
g = Graph[MeshPrimitives[reg, 1] /. Line -> Apply@UndirectedEdge, 
   VertexCoordinates -> MeshCoordinates[reg]];
faces = PlanarFaceList[g];
Graphics[{curves, HatchFilling[], EdgeForm[Cyan], 
  Polygon@faces[[2]]}]

What a useful function RegionMeshSplitIntersectingSegments[lines], didn't know it. How did you find it? — Ulrich Neumann, Feb 17 '24 at 14:59
@UlrichNeumann It is first discover by halmir https://mathematica.stackexchange.com/a/267223/72111 — cvgmt, Feb 17 '24 at 15:04
Thanks for your reply! data contains ordered linesegments and information about the intesection points. I wonder if the solution couldn't be obtained easily directly from this without the help of Graph and PlanarFaceList. — Ulrich Neumann, Feb 18 '24 at 13:29
@UlrichNeumann Only for simple n-cycle can we avoid using Planar Graph. — cvgmt, Feb 18 '24 at 14:37

cvgmt · Accepted Answer · 2024-02-22T08:48:49.967

BezierCurve can be draw as the piecewise function of the BezierFunction. When the Length of the points is 4,3,2,1, the BezierCurve or BezierFunction is the usual 3-degree Bezier curve, 2-degree parabola, Line,Point respectly. We can see this in my previous answer. https://mathematica.stackexchange.com/a/251536/72111
We use the excellent code of @Karl to simplify this case. https://mathematica.stackexchange.com/a/298382/72111

Clear["Global`*"];
bezierFunction[pts_][t_] := Module[{nd, p, n, a, b},
  nd = 3;
  n = Length@p;
  p = Partition[pts, UpTo[nd + 1], nd];
  n = Length@p;
  a = ListConvolve[{-1, 1}, 
    Prepend[UnitStep[n  t - Range[n - 1]], 1], -1, 0];
  b = MapIndexed[
    BernsteinBasis[Length@#1 - 1, Range[0, Length@#1 - 1], 
       n  t + 1 - #2[[1]]] . #1 &, p];
  PiecewiseExpand[a . b]]
pts1 = {{0, 0}, {1, 1}, {2, -1}, {3, 0}, {5, 2}, {6, -1}, {7, 3}};
pts2 = {{5, -2}, {0, 0}, {1, 2}, {5, 1}, {2, 2}, {4, 3}, {5, 4}};
pts3 = {{4, 2}, {3, 2}, {2, 3}, {-1, -3}};
curves = {curve1, curve2, curve3} = 
   BezierCurve /@ {pts1, pts2, pts3};
g = Graphics[{Arrowheads[.02], Arrow /@ curves}];
fs1 = bezierFunction[pts1];
fs2 = bezierFunction[pts2];
fs3 = bezierFunction[pts3];
intersectionPosition[f_, g_] :=
  {s, t} /. 
   Last@NMinimize[{Norm[f@s - g@t]^2, 0 < s < 1, 0 < t < 1}, {s, t}, 
     Method -> "SimulatedAnnealing"];
{{t12, t21}, {t22, t31}, {t32, t11}} = 
  intersectionPosition @@@ {{fs1, fs2}, {fs2, fs3}, {fs3, fs1}};
{{t11, t12}, {t21, t22}, {t31, t32}}
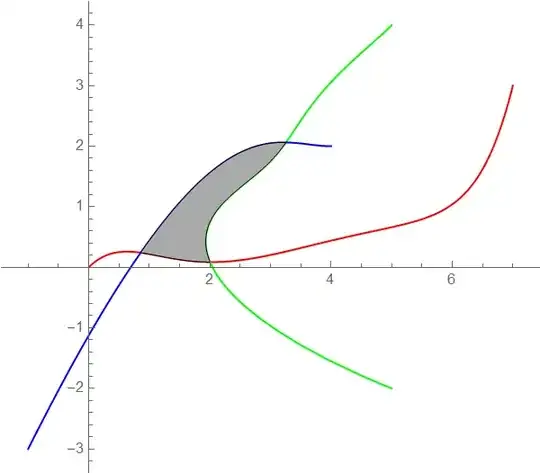
plots = {ParametricPlot[fs1@t // Evaluate, {t, t11, t12}, 
   PlotStyle -> Red], 
  ParametricPlot[fs2@t // Evaluate, {t, t21, t22}, 
   PlotStyle -> Green], 
  ParametricPlot[fs3@t // Evaluate, {t, t31, t32}, 
   PlotStyle -> Blue]}; reg = 
 Cases[Show[plots, PlotRange -> All], Line[pts_] :> pts, -1] // 
   Catenate // Polygon;
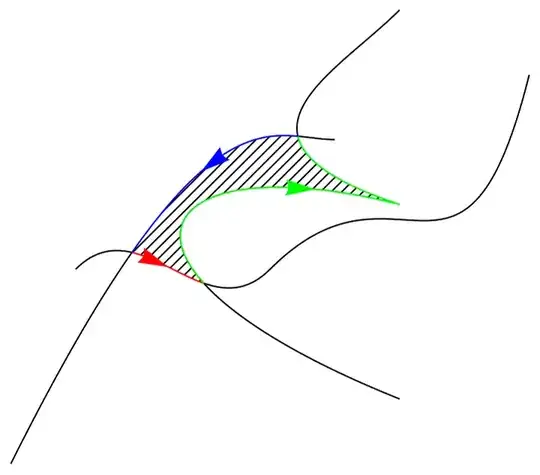
Graphics[{{HatchFilling[], reg}, curves, Arrowheads[{{Large, .5}}], 
  plots[[;; , 1]] /. Line -> Arrow}]

We can test another points.

Clear["Global`*"];
bezierFunction[pts_][t_] := Module[{nd, p, n, a, b}, nd = 3;
  n = Length@p;
  p = Partition[pts, UpTo[nd + 1], nd];
  n = Length@p;
  a = ListConvolve[{-1, 1}, 
    Prepend[UnitStep[n   t - Range[n - 1]], 1], -1, 0];
  b = MapIndexed[
    BernsteinBasis[Length@#1 - 1, Range[0, Length@#1 - 1], 
       n   t + 1 - #2[[1]]] . #1 &, p];
  a . b]
SeedRandom[123456];
pts1 = SortBy[RandomPoint[StadiumShape[{{-15, 0}, {70, 0}}, 4], 23], 
   First];
pts2 = SortBy[RandomPoint[StadiumShape[{{40, -20}, {40, 60}}, 3], 24],
    Last];
pts3 = ReverseSortBy[
   RandomPoint[StadiumShape[{{-20, -20}, {50, 50}}, 3], 23], First];
curves = {curve1, curve2, curve3} = 
   BezierCurve /@ {pts1, pts2, pts3};
fs1 = bezierFunction[pts1];
fs2 = bezierFunction[pts2];
fs3 = bezierFunction[pts3];
intersectionPosition[f_, g_] := {s, t} /. 
   Last@NMinimize[{Norm[f@s - g@t]^2, 0 < s < 1, 0 < t < 1}, {s, t}, 
     Method -> "SimulatedAnnealing"];
{{t12, t21}, {t22, t31}, {t32, t11}} = 
  intersectionPosition @@@ {{fs1, fs2}, {fs2, fs3}, {fs3, fs1}};
{{t11, t12}, {t21, t22}, {t31, t32}};
{plot1, plot2, 
   plot3} = {ParametricPlot[fs1@t // Evaluate, {t, t11, t12}, 
    PlotStyle -> Red], 
   ParametricPlot[fs2@t // Evaluate, {t, t21, t22}, 
    PlotStyle -> Green], 
   ParametricPlot[fs3@t // Evaluate, {t, t31, t32}, 
    PlotStyle -> Blue]};
{lines1, lines2, 
   lines3} = {Catenate@Cases[plot1, Line[pts_] :> pts, -1], 
   Catenate@Cases[plot2, Line[pts_] :> pts, -1], 
   Catenate@Cases[plot3, Line[pts_] :> pts, -1]};
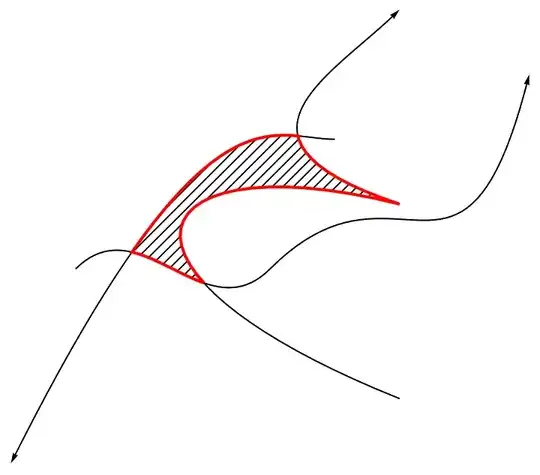
Graphics[{{HatchFilling[], Polygon@Catenate@{lines1, lines2, lines3}},
   curves, AbsoluteThickness[2], 
  Arrowheads[{{Large, .5}}], {Red, Arrow@lines1}, {Green, 
   Arrow@lines2}, {Blue, Arrow@lines3}}]

How can I build a cycled curve from three orientable Bezier curves and fill the curved region?

3 Answers3

Linked