7

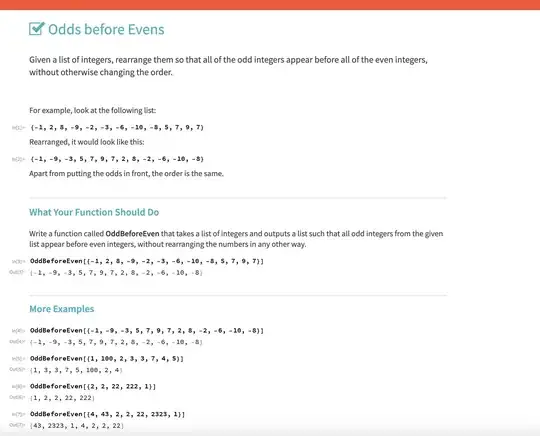
Odds before Evens Given a list of integers, rearrange them so that all of the odd integers appear before all of the even integers, without otherwise changing the order.

An obvious solution is

OddBeforeEven[data_List]:= Join[Cases[data, _?OddQ], Cases[data, _?EvenQ]]

But this isn't particularly efficient, so maybe we can try

OddBeforeEven[data_List]:= Join[Select[data, OddQ], Select[data, EvenQ]]

Now, an innovative solution could also be something like

OddBeforeEven[data_List]:= Flatten@GatherBy[data, OddQ]

But I can't seem to improve it further.

Can we optimize OddQ and EvenQ using Bit operations?

enter image description here

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
Navvye
  • 151
  • 9
  • I think it should be better to add at least an example input list of integers together with the corresponding desired result. – Αλέξανδρος Ζεγγ Feb 21 '24 at 05:30
  • Added to the post – Navvye Feb 21 '24 at 05:45
  • Just a nit... The GatherBy solution doesn't actually work in all cases. – lericr Feb 21 '24 at 15:37
  • @lericr I know. An Alternative that I found was With[{split = GroupBy[x, OddQ]}, Join[split[True], split[False]]]. It's quite annoying that the GatherBy solution doesnt work (because Wolfram sorts the association according to the number of elements in each Key)— it's very efficient and does things in a single pass. – Navvye Feb 21 '24 at 19:32
  • I don't understand your comment. GatherBy doesn't produce an association, and the lists that it does produce aren't sorted (explicitly anyway). The result of GatherBy is "sorted" according the the order in which each element was encountered. So, if the first element was odd, then the odds come first. If the first was even, then the evens come first. So, if GatherBy is your favorite, then a final pass over the results that puts the odds first before flattening would do it. – lericr Feb 21 '24 at 21:55
  • You're correct! I was confusing GroupBy and GatherBy. GatherBy is indeed my favorite – Navvye Feb 22 '24 at 20:48

4 Answers4

6
f[x_]:=x[[Join@@Lookup[PositionIndex@BitAnd[x,1],{1,0},{}]]]

f[x_]:=x[[Join@@KeySortBy[PositionIndex@BitAnd[x,1],-#&]]]

Update:

Clear["`*"]
f1[x_]:=x[[Join@@Lookup[PositionIndex@BitAnd[x,1],{1,0},{}]]]
f2[x_]:=x[[Join@@KeySortBy[PositionIndex@BitAnd[x,1],-#&]]]
f3[x_]:=Join[Select[x,OddQ],Select[x,EvenQ]]
f4[x_]:=With[{split=GroupBy[x,OddQ]},Join[split[True],split[False]]]
a=RandomInteger[100,10^7];
r1=f1@a;//RepeatedTiming
r2=f2@a;//RepeatedTiming
r3=f3@a;//RepeatedTiming
r4=f4@a;//RepeatedTiming
r1==r2==r3==r4

{0.194022, Null}

{0.19214, Null}

{2.79629, Null}

{2.01458, Null}

True

Update 2:

ClearAll["`*"]
f={x|->x[[Join@@Lookup[PositionIndex@BitAnd[x,1],{1,0},{}]]],
x|->x[[Join@@KeySortBy[PositionIndex@BitAnd[x,1],-#&]]],
x|->Join[Select[x,OddQ],Select[x,EvenQ]],
x|->With[{split=GroupBy[x,OddQ]},Join[split[True],split[False]]]};
n=10^Range[7];
t=Outer[RepeatedTiming[#1@#2;][[1]]&,f,RandomInteger[100,#]&/@n,1];
ListLogLogPlot[Inner[{#2,#1}&,t,n,List],
PlotLegends->Placed[LineLegend[ToString[#,TraditionalForm]&/@f,
LegendLayout->"Column"],Below],PlotRange->All,Joined->True,
PlotMarkers->{Automatic,Small},AxesLabel->{"n","Time(s)"}]

enter image description here

$Version

14.0.0 for Microsoft Windows (64-bit) (December 1, 2023)

Karl
  • 941
  • 1
  • 7
  • Thanks! This is a unique solution, but it's not as fast as Join[Select[list, OddQ], Select[list, EvenQ]] or the most recent addition With[{split = GroupBy[list, OddQ]}, Join[split[True], split[False]]] – Navvye Feb 21 '24 at 06:49
  • @Navvye Updated. – Karl Feb 21 '24 at 07:02
  • Very interesting! I used the benchmark set by Wolfram Challenges, and the SpeedScore was ~47 compared to 51 and 52 respectively by the abovementioned solutions. I think that the performance of your solution is best when utilized on large lists, whereas something like my solution is better for smaller lists. What do you think? – Navvye Feb 21 '24 at 07:45
  • @Navvye Updated. f1 is faster on lists ranging in length from 10 to 10^7. – Karl Feb 21 '24 at 08:03
  • could you submit your solution on Wolfram Challenges and see what the SpeedScore is? It's showing 37 for me, which is an order of magnitude less than other solutions.. Very weird!? – Navvye Feb 21 '24 at 19:33
  • @Navvye ~47.5, I don’t know exactly how the speedscore is derived, but the GroupBy one is slower than f1 on Wolfram Cloud(0.026 vs 0.36 for RandomInteger[10,10^6]) – Karl Feb 22 '24 at 03:30
3

Just a few alternatives. Nevertheless, the performance may vary depending on the list size.

l = {-1, 2, 8, -9, -2, -3, -6, -10, -8, 5, 7, 9, 7};

SortBy[{EvenQ}][l]


l[[Ordering[-BitAnd[l, 1]]]]

Result:

{-1, -9, -3, 5, 7, 9, 7, 2, 8, -2, -6, -10, -8}

vindobona
  • 3,241
  • 1
  • 11
  • 19
2

Another, Another Edit: Taking inspiration from the solution of @vindobona, I wrote

OddBeforeEven[list_]:= ReverseSortBy[{OddQ}][list]

which has a speedscore of 56.3211

Another Edit: Using Catenate is apparently faster than either Flatten or Join@@, so the fastest that I could achieve was 53.17

OddBeforeEven[list_]:= Catenate@Lookup[GroupBy[list, EvenQ], {False, True}]

Edit: Here's another one, which achieves 52.7 using GatherBy and other manipulation.

OddBeforeEven[list_]:= Flatten[Lookup[GroupBy[list,OddQ], {True, False}]]

Here's a relatively fast solution, which achieves a SpeedScore of 51.9 (the record, is 60.17)

OddBeforeEven[list_List]:= 
With[{split = GroupBy[list, OddQ]}, Join[split[True], split[False]]]
Navvye
  • 151
  • 9
1

The following code scored a respectable 54.96 in the speed test (the current highest is 60.17),

OddBeforeEven[list : {__Integer}] := 
 Block[{x = OddQ[list]}, Join[Pick[list, x], Pick[list, x, False]]]

out-performing the following (with a speed score of 51.5), which uses Mod instead of OddQ:

OddBeforeEven[list:{__Integer}]:=
  Block[{x = Mod[list, 2]}, Join[Pick[list, x, 1], Pick[list, x, 0]]]

and the following (with a score of 51.5), which uses BitAnd instead of OddQ:

OddBeforeEven[list:{__Integer}]:=
  Block[{x = BitAnd[list, 1]}, Join[Pick[list, x, 1], Pick[list, x, 0]]]

For comparison, the neat solution using Select, posted by @Navvye (in a comment), scores 51.9

OddBeforeEven[list:{__Integer}]:=
  Join[Select[list, OddQ], Select[list, EvenQ]]
user1066
  • 17,923
  • 3
  • 31
  • 49
  • 1
    Using Catenate, we can improve the speed a little bit more!

    Catenate[{Pick[list, #], Pick[list, #, False]} &@OddQ[list]]

    gives a SpeedScore of 55.07

     – Navvye Feb 23 '24 at 00:19