Defining and isolating a region of an image internal to a bounding curve

Question

I was recently looking over this very nice question by March Ho: Counting elements which are inside another element on a different colour channel

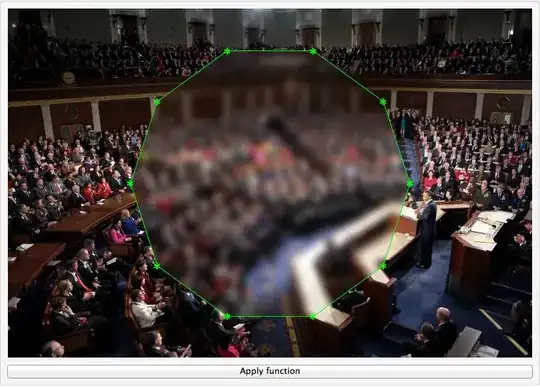
There are often times where I find myself wanting to draw a curve or define a polytope to cut out and isolate a part of an image for further analysis. One solution, for example, would be to define a set of polytope vertices, e.g.:

poly = {{658.`, 1224.`}, {672.`, 1054.`}, {507.`, 871.`}, {358.`, 876.`}, {344.`, 1432.`}, {483.`, 1410.`}};

And then calculate a winding number for each pixel in the image, or equivalently apply InPolygonQ, to define a "cutout" region. Here's a naive approach:

CutoutRegion = ImageData[pic];
ImageDimX = ImageDimensions[pic][[1]]
ImageDimY = ImageDimensions[pic][[2]]
Length[CutoutRegion[[1]]]

For[y = 1, y <= ImageDimY, y++,
  For[x = 1, x <= ImageDimX, x++,
    pt = {x, (ImageDimY-y)};
      If[Graphics`Mesh`InPolygonQ[poly, pt] == True,
       CutoutRegion[[y, x]] = 1;
       ,
       CutoutRegion[[y, x]] = 0;
      ];
  ];
 ];

ImageMultiply[Image[CutoutRegion], pic]

This works, however very slowly, and it's a little bit clumsy to define a region of interest with a polygon. Really you'd want to freehand draw something.

My question is:

• Is there a trivial way to speedup the above approach?
• Is there a more elegant way to "hand" or "mouse" define a region of interest in an image and isolate it to generate a final product similar to the output of the above approach?

Answer 1

Is there a trivial way to speedup the above approach?

You can just rasterize a polygon and use the resulting bitmap as a mask:

cutoutRegion = Binarize[Rasterize[
  Graphics[Polygon[poly],
   PlotRangePadding -> 0, 
   PlotRange -> {{0, imageDimX}, {0, imageDimY}}, 
   ImageSize -> imageDimX]]]

(btw: It's bad style to start variable names with uppercase letters)

Is there a more elegant way to "hand" or "mouse" define a region of interest in an image and isolate it to generate a final product similar to the output of the above approach?

The closest thing I'm aware of is using LocatorPane with LocatorAutoCreate -> True to enter the polygon.

Answer 2

Here's a small program I wrote for practice. It uses nikie's technique, I also used it here.

The code

locatorPositions[dim_, 0] := {};
locatorPositions[dim_, n_] := Module[{r},
  r = 0.8 Min[dim/2];
  Table[dim/2 + {r Cos[\[Theta]], r Sin[\[Theta]]}, {\[Theta], 0, 
    2 \[Pi], 2 \[Pi]/n}]
  ]
locatorConnectingLines[pos_] := Line /@ Partition[pos, 2, 1, {1, 1}];
locatorMask[dim_, pos_] := 
 ColorNegate[
  Binarize[Rasterize[
    Graphics[Polygon[pos], 
     PlotRange -> {{0, dim[[1]]}, {0, dim[[2]]}}, 
     ImageSize -> dim]]]]
locatorInterface[image_, n_, f_] := 
  DynamicModule[{dim = ImageDimensions[image], 
    pt = locatorPositions[ImageDimensions[image], n], 
    background = image},
   Panel[
    Column[
     {
      LocatorPane[
       Dynamic[pt],
       Dynamic[
        Show[background, 
         Graphics[{Green, Dynamic[locatorConnectingLines[pt]]}]]
        ], Appearance -> Style["*", Large, Green], 
       LocatorAutoCreate -> Length[pt] == 0],
      Button["Apply function", 
       background = 
        Show[background, 
         SetAlphaChannel[f[image], locatorMask[dim, pt]]]
       ]
      }
     ]
    ]
   ];

Example usage

stu = Import["http://upload.wikimedia.org/wikipedia/commons/6/65/2011_State_of_the_Union.jpg"];
locatorInterface[stu, 10, Blur[#, 12] &]

Before pressing the button:

After pressing the button:

Comments

• This is not very fast on my computer. It's probably much faster to manipulate the pixels directly.
• If you set the second argument, the number of locators, to zero, you will be able to create locators by alt-clicking or, on Mac OS, cmd-clicking.

Answer 3

Here's another approach, similar to Anon's:

i = ExampleData[{"TestImage", "Girl"}]
Manipulate[
  Row[
  {Show[
    i,
    Graphics[{Red, 
      Opacity[0.6],
      Dynamic[Polygon[u]]},
     PlotRange -> 2, 
     Background -> White]],
   Panel[result]
   }],
 {{u, {{100, 100}, {200, 200}, {200, 100}}},
  Locator,
  LocatorAutoCreate -> True},
 Button["Cookie", result = crop[i, u]], 
 Initialization :> (crop[i_, poly_] := Module[{mask},
     mask = Binarize[
       Rasterize[
        Graphics[
         Polygon[poly],
         PlotRangePadding -> 0,
         PlotRange -> Transpose[{{0, 0},
            ImageDimensions[i]}],
         ImageSize -> ImageDimensions[i]]]];
     ImageAdd[i, mask]])]

result contains the answer for further experiments...