4

The stadium billiard is a $2D$ chaotic system. We know this by studying its specular reflection patterns and Poincare section (or Poincaré-Birkhoff coordinates (PBC)). However, both methods are graphical, so one can say these are qualitative ways. Nevertheless, many authors have found a way to calculate the Lyapunov spectrum for billiards, which is considered globally a quantitative indicator of chaos.

The problem is in billiards systems, we are dealing with a functional composition of continuum and discrete maps. Every collision implies discontinuities on the trajectories.

How do you find the Lyapunov exponent for such a hybrid model? There are various papers available on this topic(Ch. Dellago et al., Phys. Rev. E 53 (1996), Ensemble separation and stickiness influence in a driven stadium-like billiard: A Lyapunov exponents analysis ). Most of them use a program written in Julia.

enter image description here

How do I develop a program in Mathematica to find the Finite Time Lyapunov Exponents(FTLE) for $2D$ billiards?

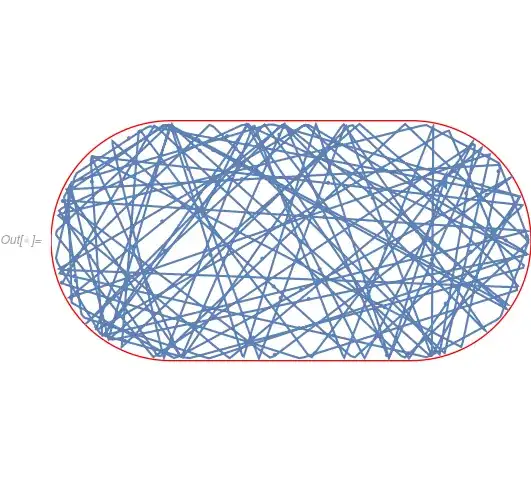
Suppose I have the following code developed by @cvgmt to find the specular reflection pattern in stadium billiard

eqn = RegionDistance[Line[{{-1, 0}, {1, 0}}], {x, y}] == 1

reg = ImplicitRegion[eqn, {x, y}];
RegionPlot[reg, AspectRatio -> Automatic]


Clear["Global`*"];
reflect[vector_, 
   normal_] = -(vector - 2 (vector - Projection[vector, normal])) // 
   Simplify;
R = StadiumShape[{{-1, 0}, {1, 0}}, 1];
R2 = RegionBoundary[R];
dist = RegionDistance[R2];
proj = RegionNearest[R2];
pt0 = RandomPoint[R, 1][[1]];
v0 = {1., 2.};
d0 = 0.01*Norm[v0];
sol = NDSolveValue[{r''[t] == {0, 0}, r[0] == pt0, r'[0] == v0, 
    WhenEvent[dist@r[t] <= d0, 
     r'[t] -> reflect[r'[t], r[t] - proj@r[t]]]}, r, {t, 0, 100}, 
   MaxStepSize -> 0.01];


Reflection = 
 Show[Graphics[{{FaceForm[White], EdgeForm[Red], R}}], 
  ParametricPlot[sol@t, {t, 0, 100}, Mesh -> {100}, 
    Method -> {"BoundaryOffset" -> False}, PlotPoints -> 80, 
    PerformanceGoal -> "Quality", PlotRange -> All] /. Line -> Arrow, 
  PlotRange -> 2]

enter image description here

How do I progress further to find the Lyapunov Exponents for this billiard or any other billiard?

user444
  • 2,414
  • 1
  • 7
  • 28
  • There are 55 questions related to the Lyapunov exponent on this site ... Does really none of the help you? – Domen Mar 11 '24 at 08:34
  • 2
    @Domen, if you look closely, then you would notice that all those questions were asked for dynamical equations (DDE or ODE) or difference equations (Maps). The problem I am having is a combination of both. Here, we deal with a functional composition of continuum and discrete maps. For more details, you can refer to the papers I've shared in the question or see this slide presentation: https://www.uv.mx/ffia/files/2021/03/Chaotic-Classical-Billiards.pdf – user444 Mar 11 '24 at 09:22
  • If using a different chaos indicators is an option, you can try REM, you need direct solution (which you have) and inverse (which seems not difficult to compute in here), only orbits are required, no tangent dynamics – I.M. Mar 12 '24 at 05:14
  • Also see this recent review paper for comparison of several indicators – I.M. Mar 12 '24 at 05:15
  • @I.M. thank you for your suggestion. Could you be able to explain a little how is this better than finding the Lyapunov spectrum? or is this simply an alternative? I'm a little sceptical as we only have reflection trajectories that are not continuous in space. So, will this method work? – user444 Mar 12 '24 at 09:18
  • It is an alternative for chaos id, if you need the exponents, this is of no use. REM method is related to the largest exponent tho, see in the rev paper. REM is easy to compute, basically given an initial $x$, compute $\hat x = \phi^{-T} \phi^{T}(x)$ (i.e. compute $x(T)$ and use it as initial in a time reversed system) and look at $|x - \hat x|$, the effect of finite precision noise is more noticable for chaotic initials. – I.M. Mar 12 '24 at 12:54

0 Answers0