How to solve two diffusion equations coupled over boundary conditions

Question

I have a two phase, ternary component system, that is recovering from an action performed on the concentration on its third component. The resulting differential equations are two coupled diffusion equations, which are coupled via boundary condition. One being equality of inward and outward flux, the other being a fixed ratio between concentration; $$\partial_t c_3(r,t) = D_1 \nabla^2 c_3 \quad for \quad r < R$$ $$\partial_t c_3(r,t) = D_2 \nabla^2 c_3 \quad for \quad r > R$$ with $$-D_1 e_r \cdot \nabla c_3 \mid_R = -D_2 e_r \cdot \nabla c_3\mid_R$$ $$c_3(r=R_-,t) = K \cdot c_3(r=R_+,t)$$ and $$\nabla c_3 \mid_{R = 0} = \nabla c_3 \mid_{R = \infty} = 0$$ where K is some number. I have attempted to solve the pde via

pde = D[T[t, x], t] ==
    D[-If[r < R, D1, D2] D[T[t, x], x], x]
FUNC = T/. NDsolve[{pde, DirichletCondition[T[r, 0] == 0, r <= R],
 DirichletCondition[T[r, 0] == 10, r > R] }, T[r,t],{r, 0, 100},{t, 0, 100}]

However I have no idea how I would introduce the second boundary condition here. Is there a way to do this? Thank you very much for your help!

Here are only conjunction condition (concentrations jump and flux continuity) on $r=R$. It seems that more BC are required. — Oleksii Semenov, Mar 11 '24 at 16:01
I tried to set arbitrary initial conditions that differ on the two regions, but to not much avail so far — IronicOwl, Mar 11 '24 at 16:51
Take a look pls at example in section Interphase Mass Transfer in documentation https://reference.wolfram.com/language/PDEModels/tutorial/MassTransport/MassTransport.html#509267359 — Oleksii Semenov, Mar 12 '24 at 10:18
As @Oleksii Semenov specified one can piece together the solution from the mass transport tutorial. — IronicOwl, Mar 18 '24 at 10:59

score 2 · Answer 1 · answered Mar 29 '24 at 10:21

As another user pointed out, one can piece together the solution from the mass transfer tutorial. This is the resulting code that worked for me:

Needs["NDSolve`FEM`"];
L = 1000;
w = 2;
leftInterphasePos = L/100 - w/2;
rightInterphasePos = L/100 + w/2;
bmesh = ToBoundaryMesh["Coordinates" -> {{0}, {leftInterphasePos}, {rightInterphasePos}, \{L}}, "BoundaryElements" -> {PointElement[{{1}, {2}, {3}, {4}}]}];
regionMarker = <|"dense" -> 1, "interphase" -> 2, "dilute" -> 3|>;
mesh = ToElementMesh[bmesh,"RegionMarker" -> {{{5}, regionMarker["dense"]}, {{10},regionMarker["interphase"]}, {{50}, regionMarker["dilute"]}}];
vars = {{Subscript[c, dense][t, x], Subscript[c, dilute][t, x]}, 
   t, {x}};
pars = <||>;
Subscript[d, dense] = If[ElementMarker == regionMarker["dense"] || 
    ElementMarker == regionMarker["interphase"], 1, 0];
Subscript[d, dilute] = If[ElementMarker == regionMarker["dilute"] || 
    ElementMarker == regionMarker["interphase"], 200, 0];
pars["DiffusionCoefficient"] = {{{{Subscript[d, dense]}}, 
    0}, {0, {{Subscript[d, dilute]}}}};
\[Sigma] = If[ElementMarker == regionMarker["interphase"], 1, 0];
k = 10^4*(Subscript[d, dense] +Subscript[d, dilute]) /. {ElementMarker-> 
     regionMarker["interphase"]};
Subscript[Q, dense] = \[Sigma]*k*(K*Subscript[c, dilute][t, x]-Subscript[c, dense][t, x]);
Subscript[Q, dilute] = \[Sigma]*k*(Subscript[c, dense][t, x]-K*Subscript[c, dilute][t, x]);
pars["MassSource"] = {{Subscript[Q, dense]}, {Subscript[Q, dilute]}};
Subscript[\[CapitalGamma], impermeable, conservative] = 
 MassImpermeableBoundaryValue[x == 0 || x == 1000, vars, pars];
ics = {Subscript[c, dense][0, x] == 0, 
   Subscript[c, dilute][0, x] == 2};
pde = {MassTransportPDEComponent[vars, pars] == Subscript[\[CapitalGamma], impermeable, conservative], ics};
tend = 1000;
cfun = ParametricNDSolveValue[pde, {Subscript[c, dense], Subscript[c, dilute]}, {t, 0,tend}, {x} \[Element] mesh, {K}];
Manipulate[Plot[Piecewise[{{cfun[10][[1]][t, x], 
     x <= leftInterphasePos}, {cfun[10][[2]][t, x], 
     x >= rightInterphasePos}, {Indeterminate, True}}], {x, 0, 50}, 
  PlotRange -> {0, 20}], {t, 0, 1000}]

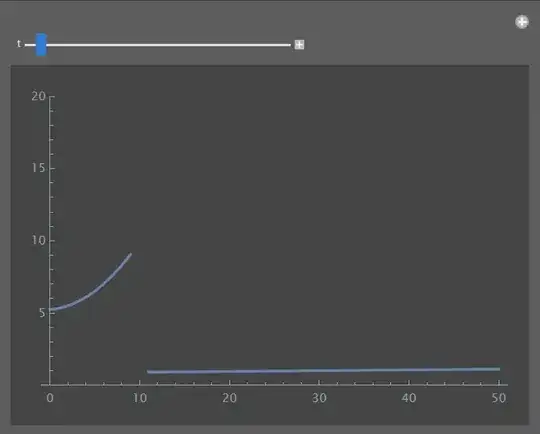
Again, this is taken almost exactly from here, with a few slight alterations to make it work for this specific problem. It produces the following manipulate;

How to solve two diffusion equations coupled over boundary conditions

1 Answers1