If you wish to interpolate on an unstructured grid then the solution is to use ElementMeshInterpolation from the Finite Element Method. I examined this here but now wish to take it further. In particular how to deal with the large aspect ratio.
I start by making some points I wish to interpolate.
pts = Table[t {Cos[t]/100, Sin[t]}, {t, 0, 100, 0.5}];
values = {#[[1]], #[[2]], #[[1]] #[[2]]^2} & /@ pts;
ListPlot3D[values, BoxRatios -> {1, 1, 1}]
The plot is poor because of the poor underlying mesh used. This can be seen if the plot is built from first principles.
Needs["NDSolve`FEM`"];
mesh = ToElementMesh[pts];
Show[mesh["Wireframe"], AspectRatio -> 1]
int = ElementMeshInterpolation[{mesh}, values[[All, 3]]];
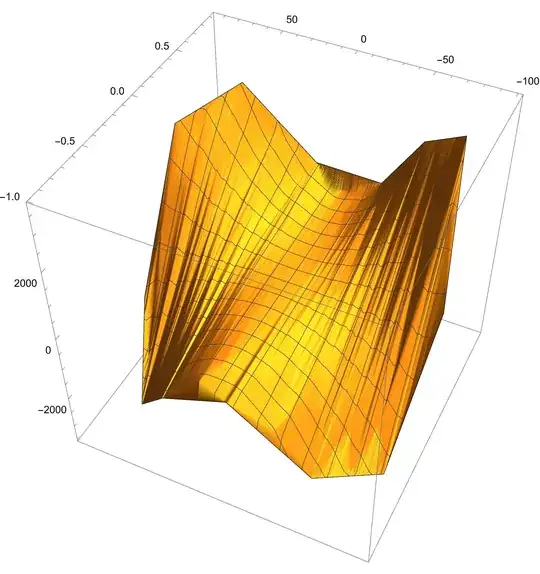
Plot3D[int[x, y], {x, y} \[Element] mesh, PlotRange -> All,
BoxRatios -> {1, 1, 1}]
The solution is to re-scale the grid points as follows
{x1, x2} = MinMax[pts[[All, 1]]];
{y1, y2} = MinMax[pts[[All, 2]]];
pts1 = {Rescale[#[[1]], {x1, x2}, {-1, 1}],
Rescale[#[[2]], {y1, y2}, {-1, 1}]} & /@ pts;
mesh1 = ToElementMesh[pts1];
Show[mesh1["Wireframe"], AspectRatio -> 1]
int1 = ElementMeshInterpolation[{mesh1}, values[[All, 3]]];
Plot3D[int1[x, y], {x, y} \[Element] mesh1, BoxRatios -> {1, 1, 1}]
This is much better although it could do with a few more points in the interpolation. The problem is now to return to the original coordinates. How do I replace the re-scaled mesh coordinates by the original coordinates?
One method is to define a remapping function as follows
ClearAll[fint];
fint[x_, y_] :=
int1[-1 + 2 (x - x1)/(x2 - x1), -1 + 2 (y - y1)/(y2 - y1)]
Show[Plot3D[fint[x, y], {x, x1, x2}, {y, y1, y2}, PlotRange -> All,
BoxRatios -> {1, 1, 1}],
Graphics3D[{PointSize[0.02], Point[values]}]
]
This is reasonable but the region of plotting or using the function has been lost. I can't define the region by {x, y} \[Element] mesh. In particular, if you save the function for future use how do you find the region from the saved values? Can one make a better interpolation function? Is there a way of putting the original coordinate values back into the function made by ElementMeshInterpolation?
Thanks




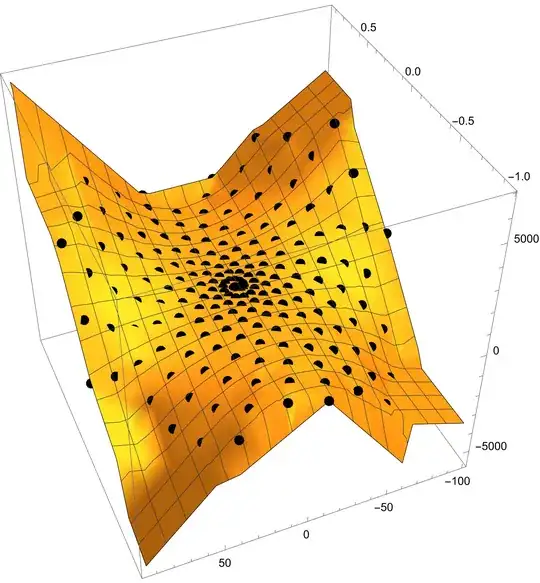
fintin a way I think you are suggesting. However, I would prefer to have a new interpolation function that does not require remapping and lets me know if my point is outside the region. – Hugh Mar 12 '24 at 14:26