I believe the culprit is differentiating usol[p][10^-10]. It looks like numerical ill-conditioning. However, I don't think differentiation should affect the numerics of the undifferentiated solution. So report it to WRI.
\[Sigma]s = .18;
{\[Alpha]2, mc} = {-0.1185, 1.27`};
bc[r_] = AiryAi[(-e mc + mc r \[Sigma]s)/(mc \[Sigma]s)^(2/3)];
inf = 20;
usol = ParametricNDSolveValue[{-(1/mc)*
D[u[r], {r, 2}] + (\[Alpha]2/r + \[Sigma]s*r)*u[r] == e*u[r],
u[inf] == bc[inf], u'[inf] == bc'[inf]}, u, {r, 10^-10, inf}, e];
p1 = Plot[usol[p][10^-10], {p, 0, 2.5}];
D[usol[p][10^-10], {p}] /. p -> 0; (*** <--- N.B.--- ***)
p2 = Plot[usol[p][10^-10], {p, 0, 2.5}, PlotStyle -> Orange];
Show[p1, p2]
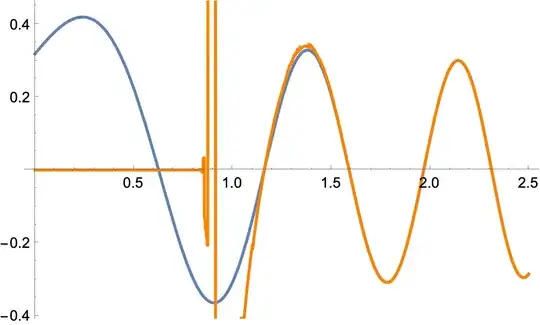
Fix one:
Don't allow differentiation (with respect to e) in ParametricNDSolve[]:
usol = ParametricNDSolveValue[{-(1/mc)*
D[u[r], {r, 2}] + (\[Alpha]2/r + \[Sigma]s*r)*u[r] == e*u[r],
u[inf] == bc[inf], u'[inf] == bc'[inf]}, u, {r, 10^-10, inf}, e,
Method -> {"ParametricSensitivity" -> None}]
Fix two:
Prevent differentiation (with respect to e) in FindRoot:
obj[p_?NumericQ] := usol[p][10^-10];
FindRoot[obj[p], {p, 2}]
Fix three:
Avoid differentiation (with respect to e) in FindRoot by using the secant method:
FindRoot[usol[p][10^-10], {p, 2, 2.1}]
Fix four:
High precision integration (lower truncation error):
\[Sigma]s = .18;
{\[Alpha]2, mc} = {-0.1185, 1.27`};
bc[r_] = AiryAi[(-e mc + mc r \[Sigma]s)/(mc \[Sigma]s)^(2/3)];
inf = 20;
usol = ParametricNDSolveValue[{-(1/mc)*
D[u[r], {r, 2}] + (\[Alpha]2/r + \[Sigma]s*r)*u[r] == e*u[r],
u[inf] == bc[inf], u'[inf] == bc'[inf]}, u, {r, 10^-10, inf}, e,
PrecisionGoal -> 12, AccuracyGoal -> 15];
p1 = Plot[usol[p][10^-10], {p, 0, 2.5}];
D[usol[p][10^-10], {p}] /. p -> 0;
p2 = Plot[usol[p][10^-10], {p, 0, 2.5}, PlotStyle -> Orange];
Show[p1, p2]
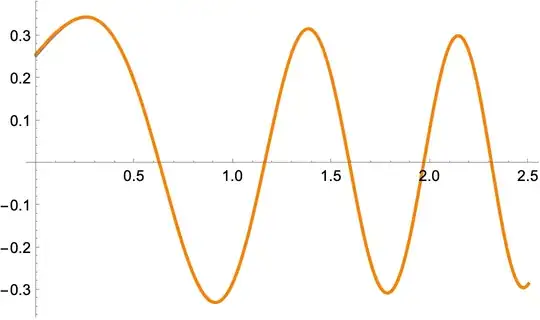
Note slight difference in plots for 0 < p < 0.1.
Fix five:
High precision numerics (lower round-off error):
\[Sigma]s = .18`32;
{\[Alpha]2, mc} = {-0.1185`32, 1.27`32};
bc[r_] = AiryAi[(-e mc + mc r \[Sigma]s)/(mc \[Sigma]s)^(2/3)];
inf = 20;
usol = ParametricNDSolveValue[{-(1/mc)*
D[u[r], {r, 2}] + (\[Alpha]2/r + \[Sigma]s*r)*u[r] == e*u[r],
u[inf] == bc[inf], u'[inf] == bc'[inf]}, u, {r, 10^-10, inf}, e,
WorkingPrecision -> 32, PrecisionGoal -> 6];
p1 = Plot[usol[p][10^-10], {p, 0, 2.532}, PlotStyle -> AbsoluteThickness[4], WorkingPrecision -> 32]; D[usol[p][10^-10], {p}] /. p -> 0; p2 = Plot[usol[p][10^-10], {p, 0, 2.532}, PlotStyle -> Orange,
WorkingPrecision -> 32];
Show[p1, p2]


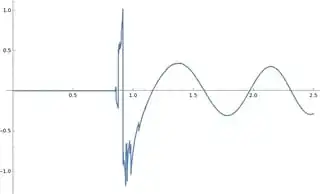





ParametricNDSolveuses caching, andFindRootseems to be evaluating the function differently, and repopulating the cache with "wrong"/less accurate values. You can doParametricNDSolve[..., Method -> {"ParametricCaching" -> None}], but I believe this should be fixed by developers, nevertheless. – Domen Mar 28 '24 at 13:12Method -> {"ParametricCaching" -> None, "ParametricSensitivity" -> None}. This should work now :) – Domen Mar 28 '24 at 17:33