FindFit: why do I get negative value as result?

Question

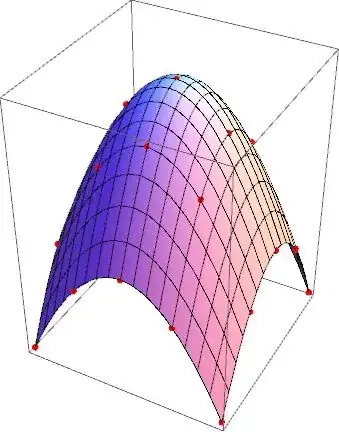
I am trying fo fit a model to data using FindFit.

J[i_, j_, α_, β_, xpos_, ypos_] := N[(β α^2*π)/4*((Erf[(j - xpos)/α ] - 
    Erf[(j + 1 - xpos)/α ])*(Erf[(i - ypos)/α ] - Erf[(i + 1 - ypos)/α ]))];

when entering the exact data Mathematica gives a negative result for parameter α.

When I put constraints on α to be positive the output is even more strange. What do I miss?

data2 = Flatten[Table[{i, j, J[i, j, 5, 20, 3.5, 3.5]}, {i, 1, 5}, {j, 1, 5}], 1]

Plane = FindFit[data2, {(β α^2*π)/4*((Erf[(j - xpos)/α ] 
  - Erf[(j + 1 - xpos)/α ])*(Erf[(i - ypos)/α ] - Erf[(i + 1 - ypos)/α ]))},
  {α, β, xpos, ypos}, {i, j}]

{α -> -4.99999, β -> 20., xpos -> 3.5, ypos -> 3.5}

thanks Now with the constrains:

Plane = FindFit[data2, {(\[Beta] \[Alpha]^2*\[Pi])/4*((Erf[(j - xpos)/\[Alpha] ] - Erf[(j + 1 - xpos)/\[Alpha] ])*(Erf[(i - ypos)/\[Alpha] ] - Erf[(i + 1 - ypos)/\[Alpha] ])), \[Alpha] > 0}, {\[Alpha], \[Beta], xpos, ypos}, {i, j}]

The output:

{\[Alpha] -> 21.4664, \[Beta] -> 58.4232, xpos -> 67.9514, ypos -> 67.9508}Plane = FindFit[data2, {(\[Beta] \[Alpha]^2*\[Pi])/4*((Erf[(j - xpos)/\[Alpha] ] - Erf[(j + 1 - xpos)/\[Alpha] ])*(Erf[(i - ypos)/\[Alpha] ] - Erf[(i + 1 - ypos)/\[Alpha] ]))}, {\[Alpha], \[Beta], xpos, ypos}, {i, j}] // Timing

{0.015600, {[Alpha] -> -5., [Beta] -> 20., xpos -> 3.5, ypos -> 3.5}}

with Method-> NMinimize we get correct solution but X60 slower...

Plane = FindFit[data2, {(\[Beta] \[Alpha]^2*\[Pi])/4*((Erf[(j - xpos)/\[Alpha] ] - Erf[(j + 1 - xpos)/\[Alpha] ])*(Erf[(i - ypos)/\[Alpha] ] - Erf[(i + 1 - ypos)/\[Alpha] ]))}, {\[Alpha], \[Beta], xpos, ypos}, {i, j}, Method -> NMinimize] // Timing

{0.624004, {\[Alpha] -> 5., \[Beta] -> 20., xpos -> 3.5, ypos -> 3.5}}

Where is that constraint of yours? Did you try given starting values for your parameters? — Sjoerd C. de Vries, Aug 19 '13 at 06:20
Thanks that helped. yet loot at the effect over the computation time: — Doron, Aug 19 '13 at 10:10
Please check here for the "easy greek letters" tool so you can edit your question. — Öskå, Aug 20 '13 at 08:21

score 1 · Accepted Answer · edited Aug 20 '13 at 08:57

To answer the question, why the value of parameter alfa is out of the reasonable range: The least squares fitting (wikipedia/list squares) must look for a global minimum of a quadratic form. In practice it may, however, stop in some local minimum, if the initial values of the parameter are in its vicinity. That is what most probably happens in your case.

For this reason you may try the parameter space for various initial values. For example, with your data I tried the following. This are your data and function:

    data2 = Flatten[
   Table[{i, j, J[i, j, 5, 20, 3.5, 3.5]}, {i, 1, 5}, {j, 1, 5}], 1];

J[i_, j_, α_, β_, xpos_, ypos_] := 
  N[(β α^2*π)/
     4*((Erf[(j - xpos)/α] - 
        Erf[(j + 1 - xpos)/α])*(Erf[(i - ypos)/α] - 
        Erf[(i + 1 - ypos)/α]))];

Here I used your FindFit statement, in which I only fixed the initial value of the "problematic" parameter alfa to 10:

    plane = FindFit[
  data2, {(β α^2*π)/
     4*((Erf[(j - xpos)/α] - 
        Erf[(j + 1 - xpos)/α])*(Erf[(i - ypos)/α] - 
        Erf[(i + 1 - ypos)/α]))}, {{α, 10}, β, 
   xpos, ypos}, {i, j}]

This is the output:

`(* {α -> 5., β -> 20., xpos -> 3.5, ypos -> 3.5}`              *)

Look at the plot here to visually judge, if the fitting is OK:

 Show[{
  Graphics3D[{Red, PointSize[Large], Point[data2]}],
  Plot3D[J[i, j, α, β, xpos, ypos] /. plane, {i, 1, 
    5}, {j, 1, 5}]}]

It should look like the following: enter image description here

To really make sure, how good is the fit with those set of parameters I would also calculate the variance or something alike fitting to your problem.

FindFit: why do I get negative value as result?

1 Answers1

Linked