I would like to (numerically) solve a forward-backward looking recurrence equation in Mathematica. The system is something like:
x[n+1] = x[n] + y[n]
y[n] = 2* y[n+1]
subject to
x[0]=1,y[N]=1
The problem is that the boundary of x at the beginning (n=0) where the boundary of y is at the end (n=N) (hence forward-backward looking). The Mathematica command RecurrenceTable does not handle this.
I would need to obtain a result for an arbitrary level of n. Numerical results are fine. What would be the most efficient method to tackle this problem?
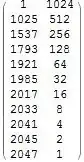
NSolveis not doing what you think it is doing. It's treatingx[n],x[n+1]etc as independent variables and just giving you a random solution to the underdetermined system. – Simon Woods Aug 23 '13 at 14:05