Cannot find the maximum value of a function

Question

Consider the following function:

$a Sin(x)+b Cos(x)$

I tried to obtain the maximum value of this function using MaxValue[]:

MaxValue[a Sin[x] + b Cos[x], x, Reals]

I expect Mathematica to return the following answer:

$\sqrt{a^2+b^2}$

But Mathematica cannot find the answer. Why does this happen?

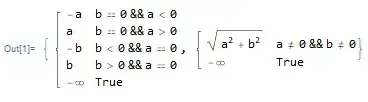
note it cant even do this: MaxValue[a Sin[x], x, Reals] – george2079 Aug 26 '13 at 15:53 — george2079, Aug 26 '13 at 15:53
@george2079 But I am puzzled, is it a bug or a feature ? – yarchik Mar 16 '17 at 20:47 — yarchik, Mar 16 '17 at 20:47

chyanog · Answer 1 · 2018-04-28T02:58:31.807

6

Try this:

MaxValue[a Sin[x] + b Cos[x] /. x -> 2 ArcTan[t] // TrigExpand, t, Reals]

MaxValue[{y, Reduce[{y == a Sin[x] + b Cos[x], #}, y, {x}, Reals]}, y]& /@
  {Xor[a == 0, b == 0], a!=0 && b!=0} // FullSimplify

edited Apr 28 '18 at 02:58

answered Aug 24 '13 at 13:55

chyanog

15,542
3
40
78

not quite.. if a==0 the max is abs[b]. I suppose because ArcTan doesn't admit the full range of angles. – george2079 Aug 24 '13 at 20:11
Thanks for the answer. The ranges of x and ArcTan[t] are different. How come x can be substituted with ArcTan[t]? – M6299 Aug 25 '13 at 05:52

score 6 · Accepted Answer · edited Aug 28 '13 at 20:26

This is essentially what b.g did, except by using Max instead of the second derivative constraint we get the result without rewriting the original expression.

f[x_] = a Sin[x] + b Cos[x];
Simplify[
    Max[f[x] /. Solve[ {f'[x] == 0 }, x] ],
       Assumptions -> {Element[a, Reals], Element[b, Reals], 
         Element[C[1], Integers]}]

Sqrt[a^2 + b^2]

I'm a bit puzzled why the conditional expression on C[1] doesn't simplify out on its own when the C[1] is gone from the expression..?

b.gates.you.know.what · Answer 3 · 2013-08-24T09:52:52.457

5

You can use a more down to earth method :

func = Sqrt[a^2 + b^2] Sin[x + f];
sol = First@Solve[{D[func, {x, 1}] == 0, D[func, {x, 2}] < 0, 
 f \[Element] Reals, a \[Element] Reals, b \[Element] Reals}, x, Reals];

Simplify[func /. sol, Assumptions -> C[1] \[Element] Integers]
(* Sqrt[a^2 + b^2] *)

edited Aug 24 '13 at 09:52

answered Aug 24 '13 at 09:41

b.gates.you.know.what

20,103
2
43
84

Would you please explain why a Sin[x] + b Cos[x] is defined as Sqrt[a^2 + b^2] Sin[x + f]. – M6299 Aug 24 '13 at 10:42
1

You can do TrigExpand[ Sin[x + f]] and match Cos[f] to a/Sqrt[a^2 + b^2] and Sin[f] to b/Sqrt[a^2 + b^2]. – b.gates.you.know.what Aug 24 '13 at 11:36

Cannot find the maximum value of a function

3 Answers3