Putting ticks with values on a parametric plot

Question

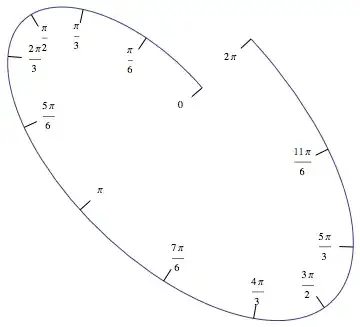
I need to plot ticks with values on the following ParametricPlot[]

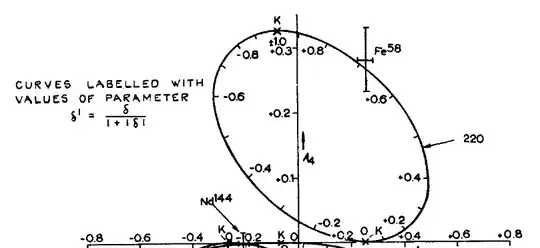
Parametric Plot of A2(gamma) and A4(gamma)

The ellipse can be obtained by

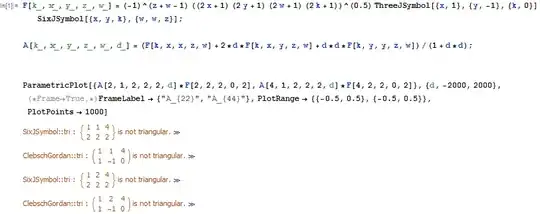
F[k_, x_, y_, z_, w_] = (-1)^(z + w - 1) ((2 x + 1) (2 y + 1) (2 w + 1) (2 k 
+ 1))^(0.5) ThreeJSymbol[{x, 1}, {y, -1}, {k, 0}] SixJSymbol[{x, y, k}, {w, w, z}];

A[k_, x_, y_, z_, w_, d_] = (F[k, x, x, z, w] + 2*d*F[k, x, y, z, w] + 
d*d*F[k, y, y, z, w])/(1 + d*d);


ParametricPlot[{A[2, 1, 2, 2, 2, d]*F[2, 2, 2, 0, 2], 
A[4, 1, 2, 2, 2, d]*F[4, 2, 2, 0, 2]}, {d, -2000, 
2000}, (*Frame->True,*) FrameLabel -> {"A_{22}", "A_{44}"},  
PlotRange -> {{-0.5, 0.5}, {-0.5, 0.5}}, PlotPoints -> 1000]

I tried it with Meshpoints, even though I need thicks with the values, and could not even figure this out. As the uploaded pictures says: The curve is labelled with values of the parameter delta' = delta/(1+|delta|). In my case delta is d.

One starting point for this might be here. – kirma Aug 30 '13 at 08:29 — kirma, Aug 30 '13 at 08:29

kirma · Accepted Answer · 2013-08-30T14:17:34.850

Partially based on Chris Degnen's answer, and all that predates it:

F[k_, x_, y_, z_, w_] =
    (-1)^(z + w - 1) ((2 x + 1) (2 y + 1) (2 w + 1) (2 k + 1))^(0.5) ThreeJSymbol[
    {x, 1}, {y, -1}, {k, 0}] SixJSymbol[{x, y, k}, {w, w, z}];

A[k_, x_, y_, z_, w_, d_] =
    (F[k, x, x, z, w] + 2*d*F[k, x, y, z, w] + d*d*F[k, y, y, z, w])/(1 + d*d);

fun[d_] := Quiet[{A[2, 1, 2, 2, 2, d]*F[2, 2, 2, 0, 2], 
    A[4, 1, 2, 2, 2, d]*F[4, 2, 2, 0, 2]}]

inward[f_, t_] := RotationTransform[\[Pi]/2][Normalize[f'[t]]]

tickGraphics[f_] := Function[{t, text},
    {Line[{f[t], f[t] + 0.02 inward[f, t]}], Text[text, f[t] + 0.05 inward[f, t]]}]

ParametricPlot[fun[d], {d, -2000, 2000}, 
    FrameLabel -> {"A_{22}", "A_{44}"}, 
    PlotRange -> {{-0.4, 0.5}, {-0.1, 0.4}}, PlotPoints -> 1000, 
    Epilog -> (tickGraphics[fun] @@@ ({d, t} /. 
        Flatten[Solve[{d/(1 + Abs[d]) == #, t == #}, {d, t}] & /@ 
            Range[-0.8, 0.8, 0.2], 1]))]

tick labels

(Feel free to clean up my code!)

And much simplified version for demonstrative purposes:

f[t_] := Evaluate[((2 \[Pi] + t)/(4 \[Pi])) RotationTransform[\[Pi]/
    4][{1, 2} RotationTransform[t][{1, 0}]]]

inward[f_, t_] := RotationTransform[\[Pi]/2][Normalize[f'[t]]]

tickGraphics[f_] := Function[t, {Line[{f[t], f[t] + inward[f, t]/10}], 
    Text[t, f[t] + inward[f, t]/5]}]

ParametricPlot[f[t], {t, 0, 2 \[Pi]}, 
    Epilog -> (tickGraphics[f] /@ Range[0, 2 \[Pi], \[Pi]/6]), 
    AspectRatio -> Automatic, Axes -> False]

simple example

Tanks guys! This is exactly what i was looking for! – Maxim Aug 30 '13 at 17:22 — Maxim, Aug 30 '13 at 17:22

Chris Degnen · Answer 2 · 2013-08-30T11:45:56.423

Further to kirma's comment:

F[k_, x_, y_, z_, 
   w_] = (-1)^(z + w - 
      1) ((2 x + 1) (2 y + 1) (2 w + 1) (2 k + 
        1))^(0.5) ThreeJSymbol[{x, 1}, {y, -1}, {k, 0}] SixJSymbol[{x,
      y, k}, {w, w, z}];

A[k_, x_, y_, z_, w_, 
   d_] = (F[k, x, x, z, w] + 2*d*F[k, x, y, z, w] + 
     d*d*F[k, y, y, z, w])/(1 + d*d);

Quiet[fun = {A[2, 1, 2, 2, 2, d]*F[2, 2, 2, 0, 2], 
    A[4, 1, 2, 2, 2, d]*F[4, 2, 2, 0, 2]}];

Show[ParametricPlot[fun, {d, -2000, 2000},(*Frame\[Rule]True,*)
  FrameLabel -> {"A_{22}", "A_{44}"}, 
  PlotRange -> {{-0.5, 0.5}, {-0.5, 0.5}}, PlotPoints -> 1000],
 ListPlot[
  fun /. Solve[d/(1 + Abs[d]) == #, d] & /@ Range[-0.8, 0.8, 0.2], 
  PlotStyle -> Hue[0.67, 0.6, 0.6], PlotMarkers -> "\[FilledCircle]"],
  PlotRange -> {{-0.5, 0.5}, {0, 0.5}}]

enter image description here

Show[ParametricPlot[fun, {d, -2000, 2000},(*Frame\[Rule]True,*)
  FrameLabel -> {"A_{22}", "A_{44}"}, 
  PlotRange -> {{-0.5, 0.5}, {-0.5, 0.5}}, PlotPoints -> 1000],
 Graphics[
    Rotate[Translate[Line[{{-0.01, 0}, {0.01, 0}}], #1], 
     ArcTan @@ #2]] & @@@ 
  Flatten[{fun, RotationMatrix[\[Pi]/2].D[fun, d]} /. 
      Solve[d/(1 + Abs[d]) == #, d] & /@ Range[-0.8, 0.8, 0.2], 1], 
 PlotRange -> {{-0.5, 0.5}, {0, 0.5}}]

enter image description here

Putting ticks with values on a parametric plot

2 Answers2

Linked