Pick elements of largest absolute value

Question

For example, given

list = {{1, -3, -5}, {2, 1, 6}, {0, 2, 4}, {-9, 2, 6}}

should return:

{-5, 6, 4, -9}

Updated

I found a undocumented function called Internal`MaxAbs,but it only accept two args，for example：

Internal`MaxAbs[2, -3]
Internal`MaxAbs[{1, -3, -5}, {2, 1, 6}]
(*
 3
 {2, 3, 6}
*)

How can I make it can accept multiple parameters?

Answer 1

(Edited with a slight tweak for a tiny bit more speed)

For the non-duplicate version I am finding this quite fast:

f = If[+## > 0, ##] & @@ {Max[#], Min[#]} &

f /@ list
(* {-5, 6, 4, -9} *)

Answer 2

I'd use Ordering, as Nasser did, but with the default sort as it will be much faster:

# ~Extract~ Ordering[Abs@#, -1] & /@ list

{-5, 6, 4, -9}

If duplicates are required we can substitute Position but Pinguin Dirk's method is faster.

list = {{1, -3, -5}, {2, 1, 6}, {0, 2, 4}, {-9, 2, 6}, {1, -2, 2}}

# ~Extract~ (Position[#, Max@#] &@Abs@#) & /@ list

{{-5}, {6}, {4}, {-9}, {-2, 2}}

---

Here is a concise use of Pick that appears to be competitive for the with-duplicates case:

f[a_] := Pick[a, #, Max@#] & @ Abs @ a

f /@ list

{{-5}, {6}, {4}, {-9}, {-2, 2}}

Timings in version 7 (Pick should be faster in v8 and after):

SetAttributes[timeAvg, HoldFirst]
timeAvg[func_] := Do[If[# > 0.3, Return[#/5^i]] & @@ Timing@Do[func, {5^i}], {i, 0, 15}]

list = RandomInteger[{-30, 30}, {50000, 20}];

# ~Extract~ (Position[#, Max@#] &@Abs@#) & /@ list  // timeAvg
Pick[list, UnitStep[# - Max[#]] & /@ (Abs@list), 1] // timeAvg
f /@ list                                           // timeAvg

0.2496

0.2184

0.1996

Nasser's timings in version 9 are: 0.328, 0.112, 0.203 showing that Pinguin Dirk's code is by far the fastest in recent versions.

And timings for the non-duplicate methods:

list = RandomReal[{-9, 9}, {50000, 20}];

# ~Extract~ Ordering[Abs@#, -1] & /@ list                                  // timeAvg
(SortBy[#, Abs] & /@ list)[[All , -1]]                                     // timeAvg
If[+## > 0, ##] & @@ {Max[#], -Max[-#]} & /@ list                          // timeAvg
Pick[Flatten@#, Flatten[Ordering@Ordering@Abs[#] & /@ #], 3] &@list        // timeAvg
MapThread[Extract, {list, Ordering[#, -1, (Abs@#1 < Abs@#2) &] & /@ list}] // timeAvg
Max /@ Pick[list, UnitStep[# - Max[#]] & /@ (Abs@list), 1]                 // timeAvg

0.078

0.1092

0.128

0.2308

0.842

0.2652

Answer 3

With the clarification, I think I can reuse my solution I initially provided by just mapping Max over it again:

Old:

Pick[list, UnitStep[# - Max[#]] & /@ (Abs@list), 1]

New:

Max /@ Pick[list, UnitStep[# - Max[#]] & /@ (Abs@list), 1]

(note: the old solution returned any value that has max abs value, i.e. {1,2,-2} returned 2,-2).

Based on this new information, this approach is definitely not the best out there, see @Mr.Wizard's answer.

Answer 4

Update: Added to test table below new 3 answers.

I came up with an improvement to my earlier method. Instead of running the Ordering on the original list, why not run it on a much smaller list? of only 3 items !

This new list is first generated from the original list like this:

{Abs[#], Max[#], Min[#]} & /@ list

Now with only 3 elements in each list, it is much faster to do the same thing as before. The idea is to check if first element same as Abs of 3rd element. If not, then use the middle element, else use the third. So it is only an If added to each element. Min/Max/Abs so the heavy work:

If[#[[1]] == Abs@#[[3]],#[[3]], #[[2]]] & /@({Max@Abs[#], Max[#], Min[#]}& /@ list) 

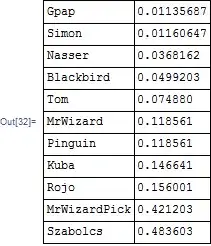
UPDATE TIMING

All run on V 9.01, windows 7, 64 bit. Intel core i7. Using this list

  list = RandomInteger[{-30, 30}, {50000, 20}];

Using this list

list = RandomReal[{-9, 9}, {50000, 20}];

Appendix

Test code:

SetAttributes[timeAvg, HoldFirst]
timeAvg[func_] := 
 Do[If[# > 0.3, Return[#/5^i]] & @@ Timing@Do[func, {5^i}], {i, 0, 15}]
MrWizardPick[a_] := Pick[a, #, Max@#] &@Abs@a  ;
(*list=RandomInteger[{-30,30},{50000,20}];*)
MaxBy[list_, fun_] := list[[First@Ordering[fun /@ list, -1]]];
list = RandomInteger[{-30, 30}, {50000, 20}];
gpap = Block[{M, m}, M = Max@#;
    m = Min@#;
    If[M > -m, M, m]] &;

Grid[{
  {"Gpap", gpap /@ list // timeAvg},
  {"Simon", If[+## > 0, ##] & @@ {Max[#], Min[#]} & /@ list // timeAvg},
  {"Nasser", If[#[[1]] == Abs@#[[3]], #[[3]], #[[2]]] & /@ ({Max@Abs[#], Max[#], 
         Min[#]} & /@ list) // timeAvg},
  {"Blackbird",Table[If[
      Min[list[[i]]] < 0 && Abs[Min[list[[i]]]] > Max[list[[i]]], 
      Min[list[[i]]], Max[list[[i]]]], {i, Length[list]}] // timeAvg},
  {"Tom",Pick[Flatten@#, Flatten[Ordering@Ordering@Abs[#] & /@ #], 3] &@ list // timeAvg},
  {"MrWizard", #~Extract~Ordering[Abs@#, -1] & /@ list // timeAvg},
  {"Pinguin",Max /@ Pick[list, UnitStep[# - Max[#]] & /@ (Abs@list), 1] // timeAvg},
  {"Kuba", (SortBy[#, Abs] & /@ list)[[;; , -1]] // timeAvg},
  {"Rojo", Pick[list, 
      With[{absList = Abs@list}, 
       With[{max = Max /@ absList}, # - max & /@ Transpose@absList] //
          Unitize // Transpose], 0] // Flatten // timeAvg},
  {"MrWizardPick", MrWizardPick /@ list // timeAvg},
  {"Szabolcs", MaxBy[#, Abs] & /@ list // timeAvg}
  }, Frame -> All, Alignment -> Left, Spacings -> {.5, 1}]

Answer 5

Using the function introduced here, it becomes a trivial exercise:

MaxBy[#, Abs] & /@ list

(* ==> {-5, 6, 4, -9} *)

It's probably not the fastest, but if you're familiar with the pattern, it's the least mental effort solution.

Answer 6

list = {{1, -3, -5}, {2, 1, 6}, {0, 2, 4}, {2, -9, 6}};

One way would be:

(SortBy[#, Abs] & /@ list)[[;; , -1]]

{-5, 6, 4, -9}

But I bet it is not effective since we do not have to sort each list to obtain this. However for short sublists it may be good approach.

---

Ok, this scans only once but maybe MapIndexed is not the fastest scanner:

max[_] = 0;
f[z_, {i_, j_}] := max[i] = If[Abs[max[i]] > Abs@z, max[i], z]

MapIndexed[f, list, {2}];

max /@ Range[Length[list]]

{-5, 6, 4, -9}

Answer 7

Ok, so a bit late but I want to play as well. It's a variation on a theme by @SimonWoods:

ClearAll@f

f = Block[{M, m},
   M = Max@#;
   m = Min@#;
   If[M < -m, m, M]
   ] &

but in my machine it works slightly faster.

list = {{1, -3, -5}, {2, 1, 6}, {0, 2, 4}, {-9, 2, 6}};
f /@ list
(*out*) {-5, 6, 4, -9}

--EDIT--

Changed If[M > -m, M, m] to If[M < -m, m, M] to pick the positive of two numbers with equal absolute value.

Answer 8

I'll join the fun:

r = Ordering[#, -1, (Abs@#1 < Abs@#2) &] & /@ list;
MapThread[Extract, {list, r}]

Answer 9

More fun:

Pick[Flatten@#, Flatten[Ordering@Ordering@Abs[#] & /@ #], 3] &@list

=> {-5, 6, 4, -9}

Answer 10

I saw so many answers that I just had to participate. This won't work for a ragged array

Pick[list,
  With[{absList = Abs@list},
   With[{max = Max /@ absList},
      # - max & /@ Transpose@absList] // Unitize // Transpose
   ], 0] // Flatten

Answer 11

Table[If[Min[list[[i]]] < 0, Min[list[[i]]], Max[list[[i]]]], {i, 
  Length[list]}]

{-5, 6, 4, -9}

For list = RandomInteger[{-30, 30}, {50000, 20}];

Time = 0.040058

list = RandomReal[{-9, 9}, {50000, 20}];

Time = 0.050072

Edit: As a valid mistake found by @simonWoods, I have rectified the snippet and now its generating better result.

Table[If[Min[list[[i]]] < 0 && Abs[Min[list[[i]]]] > Max[list[[i]]], 
  Min[list[[i]]], Max[list[[i]]]], {i, Length[list]}]

For list = {{-1, 10}}; (*{10}*)

For list = {{1, -3, -5}, {2, 1, 6}, {0, 2, 4}, {-9, 2, 6}} (*{-5, 6, 4, -9}*)

For list = {{-1, -10, 10}}; (*{10}*)

For list = RandomInteger[{-30, 30}, {50000, 20}];

Time = 0.120173

For list = RandomReal[{-9, 9}, {50000, 20}];

Time = 0.130187(Ranging from .012.. to .014.. on my system)

Answer 12

One way to ensure the + wins in the case of equal Abs..

(Last@SortBy[ #, {Abs[#], #} & ]) & /@
   {{1, 2, -2}, {1, 5, -5}, {1, -3, 3}, {1, -4}}

(* {2, 5, 3, -4} *)

or this may be faster..dont feel like running for time.

(Last@SortBy[{Max[#], Min[#]}, Abs]) & /@
  {{1, 2, -2}, {1, -5, 5}, {1, -3, 3}, {1, -4}}

Edit -- oops not nesessary SortBy autmaticaly breaks the tie based on signed value so just this works..

(Last@SortBy[ #, Abs ]) & /@
   {{1, 2, -2}, {1, 5, -5}, {1, -3, 3}, {1, -4}}

" If some of the f[e_i] are the same, then the canonical order of the corresponding e_i is used. "

Answer 13

In versions 10+, you can use MaximalBy and TakeLargestBy:

list = {{1, -3, -5}, {2, 1, 6}, {0, 2, 4}, {-9, 2, 6}};

Flatten[MaximalBy[Abs]/@list]

 {-5, 6, 4, -9}

Flatten[TakeLargestBy[Abs, 1]/@list]

 {-5, 6, 4, -9}

TakeLargestBy is the faster of the two. Both are much slower than other methods posted so far.

Answer 14

As first pointed out by @rm-rf, there exist internal, undocumented functions Random`Private`MapThreadMin and Random`Private`MapThreadMax, and these are useful for this purpose. Here is a function that uses these internal functions:

maxByAbs[list_] := With[{t = Transpose@list},
    With[{min = Random`Private`MapThreadMin[t], max = Random`Private`MapThreadMax[t]},
        max + UnitStep[Abs[min] - max] (min-max)
    ]
]

The basic idea is to get the minimum and maximum values of each list, and then use arithmetic to figure out which one is larger. Here is the OP example:

maxByAbs[{{1, -3, -5}, {2, 1, 6}, {0, 2, 4}, {-9, 2, 6}}]

{-5, 6, 4, -9}

And here is a brief timing comparison with the chosen answer:

list=RandomInteger[{-30,30}, {50000,20}];

f = If[+## > 0, ##] & @@ {Max[#], Min[#]} &;

r1 = f/@list; //RepeatedTiming
r2 = maxByAbs[list]; //RepeatedTiming

r1===r2

{0.0068, Null}

{0.0028, Null}

True