Title says it all. Mathematica produces sometimes expressions of the form
Abs[a + Exp[I*c]b]^2
where all three quantities a, b and c are positive real numbers. That expression of course reduces simply to the law of cosines
a^2 + b^2 + 2a b Cos[c]
however, I cannot get Mathematica to display it in this form. Any ideas?
Not sure why all responses here are not simple and direct, maybe in older versions this did not work, but now it does:
Abs[a+Exp[I*c] b]^2//ComplexExpand//FullSimplify
a^2+b^2+2 a b Cos[c]
(Abs[a+Exp[I*c] b]^2+Abs[a-Exp[I*c] b]^2)/(2 Abs[a+I b]^2)//ComplexExpand//FullSimplify
1
$Version
14.0.0 for Mac OS X x86 (64-bit) (December 1, 2023)
Until someone figures out how to do it in a better way, here is a work around. Define a function (which is true only for your specific case of parameters):
RemoveAbs[x_] := FullSimplify[ComplexExpand[Sqrt[x Conjugate[x]]]]
Then
Abs[a + Exp[I*c] b]^2 /. Abs -> RemoveAbs
a^2 + b^2 + 2 a b Cos[c]
There is a simpler version inspired by @Nasser answer. Define a function
RemoveAbs[x_] := ComplexExpand[Abs[x]]
and now, for the sake of variety, apply simplification at the end:
Abs[a + Exp[I*c] b]^2 /. Abs -> RemoveAbs // FullSimplify
a^2 + b^2 + 2 a b Cos[c]
Point is, all the above will work for more complicated cases because /. is a ReplaceAll. Even for cases that are convoluted via things like, for example, TraditionalForm - the only thing you need is that InputForm still has Abs in it. For instance, imagine a beast of expression, here rather a simpler one but in reality they could go for pages:
(Abs[a + Exp[I*c] b]^2 + Abs[a - Exp[I*c] b]^2)/(2 Abs[a + I b]^2) // TraditionalForm
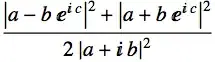
and now, voila, you get your simplification:
% /. Abs -> RemoveAbs // FullSimplify
1
ClearAll[a, c, b];
expr = a + Exp[I*c] b;
Simplify@Expand@(ComplexExpand[Abs@expr]^2)
Or in non @ friendly way
Simplify [ Expand [ ComplexExpand[Abs[expr]]^2 ] ]
I like very much the solution of Nasser, especially since it is direct, i.e. it does not use any workaround, but just the Mathematica technique. Not to leave such a basic exercise with only one solution I would like to offer a very simple one:
Clear[exprA, exprB];
exprA = a + Exp[I*c] b
exprB = exprA /. c -> -c (* This produces the conjugated expression *)
(* a + b E^(I c) *)
(* a + b E^(-I c) *)
Now let us recall that Abs[z]^2=z z* and just multiply
ComplexExpand[exprA*exprB] // Simplify
(* a^2 + b^2 + 2 a b Cos[c] *)
It should be noted that I used the replacement c->-c to obtain the conjugated value using that it is known all parameters to be positive, including c. It can be done in a more general way using Conjugate[]. In this case the final result is the same, but the intermediate results (if one chooses to look at them) are more cumbersome. Anyway,
ComplexExpand[exprA*Conjugate[exprA]] // Simplify
(* a^2 + b^2 + 2 a b Cos[c] *)
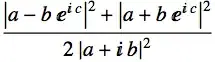
Abs[a + Exp[I*c]b]^2. Just noting the difference, but this may work for him too. – Vitaliy Kaurov Sep 01 '13 at 05:11ComplexExpandon something before squaring, vs. squaring then applyingComplexExpand(which will not have simplified). Mathematically these seem to be the same to me sinceComplexExpanddoes not add or take anything, but modifies the shape of the expression. But may be I am missing something. – Nasser Sep 01 '13 at 05:29