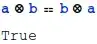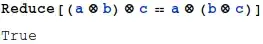I am currently running Mathematica 8 and I would like to know how to define custom operators.
Let's say I define an operator called $\times$ where:
$$a\times b = a+a\cdot b+b$$
I also want to know if it is commutative, associative, its inverse, identity and whether it is closed for Z. How would I do that in Mathematica.
For the first part of your question please see a very recent Q&A:
"How is + as an infix operator associated with Plus?"
There you will find everything about defining operators yourself. For the second part, lets use your definition and bind it to CircleTimes.
CircleTimes[a_, b_] := a + a*b + b;
Now you can verify some of your assumptions. I use images instead of code-blocks, so that you see the rendered output. The operator can be inserted with the combination Esc+c+*+Esc. Verify commutativity:
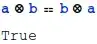
associativity
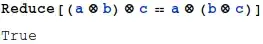
Inverse element which does not necessarily exist in $\mathbb{Z}$
and the identity can be calculated likewise. I don't know whether you can show with Mathematica that this operator is closed in $\mathbb{Z}$, but you could easily make this clear, since you only use + and * which is closed in $\mathbb{Z}$.
I hope this gives you some point to start.
