How to simplify my expression to the style of "a+b*I"?

Question

How to simplify my expression to the style of "a+b*I"?

Expand[(E^(I θ) (-1 + E^(I n θ)))/(-1 + E^(I θ))]

-(E^(I θ)/(-1 + E^(I θ))) + E^(I θ + I n θ)/(-1 + E^(I θ))

Answer 1

I hope this is what you need:

Collect[Expand[(E^(I \[Theta]) (-1 + E^(I n \[Theta])))/(-1 + 
      E^(I \[Theta]))] // ComplexExpand, I]

Answer 2

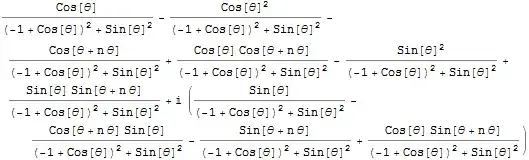
As shown by others, you are looking for a combination of ComplexExpand and Collect. In your case, ComplexExpand does a good job of separating the real and imaginary components of your expression.

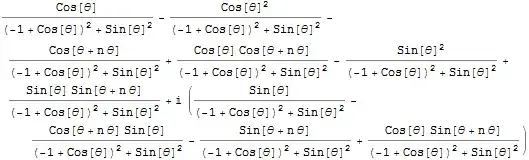
In general, you will end up with a number of terms, and you will need to use Collect to merge them together. However, using Collect on I does not usually work

Collect[a I + (1 + I) b, I]
(* I a + (1 + I) b *)

because I is interpreted as Complex[0, 1], so Collect will not break up numbers like 1 + I. So, the most effective method I have found is to replace I with some other symbol, like q.

Block[{q}, 
  Collect[
   ComplexExpand[expr] /. Complex[a_, b_] :> a + q b, 
   q, Simplify
  ] /. q -> I
]
(*
    Cos[1/2 (1 + n) θ] Csc[θ/2] Sin[(n θ)/2] 
+ I Csc[θ/2] Sin[(n θ)/2] Sin[1/2 (1 + n) θ]
*)

where expr is your expression. Note I set the third argument of Collect to Simplify which reduced the complexity of the real and imaginary parts quite well.

Answer 3

exp = Expand[(E^(I \[Theta]) (-1 + E^(I n \[Theta])))/(-1 +E^(I \[Theta]))]

r = Simplify@ComplexExpand@Re@exp + I*Simplify@ComplexExpand@Im@exp

it is now in the form a+I b

{a, b} = First@Cases[r, Plus[a_, I b_] :> {a, b}, {0}];
a

b