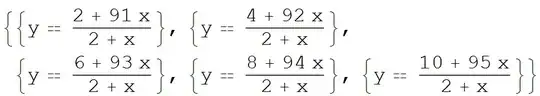Is there a triangle like this?

Question

I want to find the numbers $a$, $b$, $c$, $d$ of the function $y = \dfrac{a x + b}{c x + d}$ so that the triangle $ABC$ with three points $A$, $B$, $C$ have integer coordinates and lies on the graph of the given function, then the centroid of the triangle $ABC$ (have also integer coordinates) is also lies on the graph. I tried

Clear[f, m, n, p];
f[x_] := (a x + b)/(c x + d);
m = {h, k};
n = {e, f};
p = {(m[[1]] + n[[1]] + x)/3, (f[m[[1]]] + f[n[[1]]] + f[x])/3}
Reduce[{p[[2]] == f[p[[1]]], f[h] == k, f[e] == f, 
Sequence @@ Thread[0 < {a, b, c, d, e, f, h, k, x} < 10], 
a < b < c < d}, {a, b, c, d, e, f, h, k, x}, Integers]

With my code, I get the answer is False. Is there a triangle like this?

Are there any examples if you relax the integer constraint? – bill s Sep 14 '13 at 16:18 — bill s, Sep 14 '13 at 16:18
This seems like it would fit well in the Mathematics site. – DavidC Sep 14 '13 at 16:54 — DavidC, Sep 14 '13 at 16:54

Dr. belisarius · Accepted Answer · 2015-07-11T13:55:30.293

23

Edit

A new solution (no luck is needed now :P ):

g[x_] := (a x + b)/(c x + 1); (*d is a scale factor or zero*)
cent[x1_, x2_, x3_] := 1/3  ({x1, g[x1]} + {x2, g[x2]} + {x3, g[x3]});
fi = First@FindInstance[{
     g@First@cent[x1, x2, x3] == Last@cent[x1, x2, x3],
     a/b != c != 0, x1 != x2 != x3,
     Element[{x1, x2, x3, g[x1], g[x2], g[x3],Sequence @@ cent[x1, x2, x3]}, Integers]},
    {x1, x2, x3, a, b, c}, Reals];
Grid@{
   {"p1", {x1, g[x1]}},
   {"p2", {x2, g[x2]}},
   {"p3", {x3, g[x3]}},
   {"Centroid", cent[x1, x2, x3]}} /. fi

\begin{array}{cc} \text{p1} & \{6,-6585\} \\ \text{p2} & \{0,-85\} \\ \text{p3} & \{9,1540\} \\ \text{Centroid} & \{5,-1710\} \\ \end{array}

x = {{x1, g[x1]}, {x2, g[x2]}, {x3, g[x3]}};
IntegerQ /@ (Flatten@Join[x, {cent[x1, x2, x3]}] /. fi)

{True, True, True, True, True, True, True, True}

Mathematica graphics

Grid@{{"a", a}, {"b", b}, {"c", c}} /. fi // TeXForm

\begin{array}{cc} \text{a} & -59 \\ \text{b} & -85 \\ \text{c} & -\frac{7}{45} \\ \end{array}

edited Jul 11 '15 at 13:55

answered Sep 14 '13 at 17:12

Dr. belisarius

115,881
13
203
453

Why don't you have it print out the x,y coordinates of the vertices. – DavidC Sep 14 '13 at 17:27
@DavidCarraher Done – Dr. belisarius Sep 14 '13 at 17:28
Amazing, weird result. I'm impressed. – m_goldberg Sep 14 '13 at 23:04
@m_goldberg I really started trying to find a stronger evidence for the nonexistence, but ... – Dr. belisarius Sep 15 '13 at 17:13
Very nice, indeed. – Eckhard Sep 15 '13 at 17:30
@belisarius Can I get a triangle with the small coordinates of the point A, B, C? – minthao_2011 Sep 17 '13 at 04:39
@minthao_2011 for {x1 -> -1, x2 -> -5, x3 -> 0, a -> 26, b -> -38, c -> 7/5} you get {g[x1], g[x2], g[x3]} -> {160, 28, -38}. Is that small enough? – Dr. belisarius Sep 17 '13 at 11:53
How to choose the number a, b, c, x1, x2, x3? – minthao_2011 Sep 17 '13 at 12:29
@minthao_2011 The solutions come from the FindInstance code above. I have no explicit formula – Dr. belisarius Sep 17 '13 at 12:30
The solutions changes automatically? Is it fixed? How to change it? – minthao_2011 Sep 17 '13 at 12:34
@minthao_2011 Try FindInstance[{ y == First@cent[x1, x2, x3, 1], g[y] == Last@cent[x1, x2, x3, 1], a != c, c != 0, a/b != c/d}, {x1, x2, x3, y, a, b, c, d}, Reals, 2] The last "2" is for getting two solutions, and so on – Dr. belisarius Sep 17 '13 at 12:36

minthao_2011 · Answer 2 · 2013-09-23T15:19:53.857

My student found a function $y = \dfrac{93 x + 6}{x+2}$. Then, $A(-6,138)$, $B(8,75)$, $C(-62,96)$ and centroid $G(20,103)$. And he found a general formulas in order to find the coefficients $a$, $b$, $d$ if choice $c= 1$. Another functions from the following code

{y == (a x + b)/(c x + d)} /. Solve[{a d - b == 180, 90 <= a <= 180, c == 1, 1 <= b <= 10, 1 <= d <= 10}, {a, b, d}, Integers]

enter image description here

Try this code

Clear[f, a, b, c, g];
f[x_] := (19 x + 10)/(x + 10);
a = {x1, f[x1]};
b = {x2, f[x2]};
c = {x3, f[x3]};
g = 1/3 {x1 + x2 + x3, f[x1] + f[x2] + f[x3]}
{a, b, c, g} /. 
Solve[{g[[2]] == f[g[[1]]], 
Sequence @@ Thread[-200 < {x1, x2, x3} < 200], x1 < x2 < x3}, {x1, x2, x3}, Integers]

I want to the numbers a, b, d and coordinates of point A, B, C, G are smaller. Another function is f[x_] := (11 x + 1)/(7 x + 17);

Is there a triangle like this?

2 Answers2