Intersection of two functions in SphericalPlot3D

Question

How do I draw the intersection of these functions?

SphericalPlot3D[{Csc[ϕ], Sqrt[2]}, {θ, 0, 2 π}, {ϕ, 0, π}, 
    BoxRatios -> {1, 1, 1}, AxesLabel -> {x, y, z}, Mesh -> None, 
    PlotRange -> {-1.5, 1.5}, PlotStyle -> Directive[Blue, Opacity[0.1]]]

If you can convert them to implicit forms, you can use the techniques in answers to this question — rm -rf, Sep 15 '13 at 19:26
I've seen the question before asking. I've tried to get the form, but it's another problem. — user28936, Sep 15 '13 at 20:02

Michael E2 · Accepted Answer · 2013-09-15T20:24:34.823

You can use MeshFunctions on one of the plots, adapting the other function for the mesh function.

With[{opts = {BoxRatios -> {1, 1, 1}, AxesLabel -> {"x", "y", "z"}, 
    PlotRange -> {-1.5, 1.5}, PlotStyle -> Directive[Blue, Opacity[0.1]]}},
 Show[
  SphericalPlot3D[
   Csc[φ], {θ, 0, 2 π}, {φ, 0, π}, 
   Mesh -> None, opts],
  SphericalPlot3D[Sqrt[2], {θ, 0, 2 π}, {φ, 0, π},
   Mesh -> {{0.}}, 
   MeshFunctions -> {Function[{x, y, z, θ, φ, r}, 1/r - Sin[φ]]},
   BoundaryStyle -> None, opts]
  ]
 ]

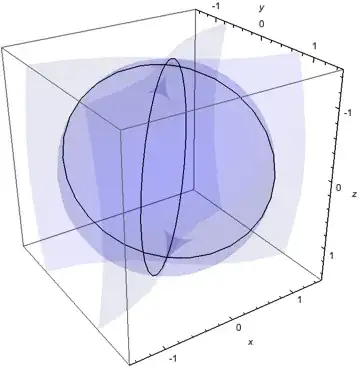
Mathematica graphics

Or, in this case, one could solve explicitly for the intersection (φ equals π/4, 3π/4).

SphericalPlot3D[{Csc[φ], Sqrt[2]},
 {θ, 0, 2 π}, {φ, 0, π},
 BoxRatios -> {1, 1, 1}, AxesLabel -> {"x", "y", "z"},
 Mesh -> {{π/4, 3 π/4}}, MeshFunctions -> {Function[{x, y, z, θ, φ, r}, φ]}, 
 PlotRange -> {-1.5, 1.5}, PlotStyle -> Directive[Blue, Opacity[0.1]],
 BoundaryStyle -> None]

Sometimes it is necessary to increase PlotPoints to get a smooth mesh line for the intersection.

You can plot the intersection without the surface with the setting PlotStyle -> None.

Intersection of two functions in SphericalPlot3D

1 Answers1