4

I'm trying to figure out how to use FindFit with a multivariable differential equation model and data. I've successfully made it work for the one-variable version of the model by following the example on the Help page: 

DNA = 10;

model[ a_?NumberQ, b_?NumberQ, c_?NumberQ, d_?NumberQ, f_?NumberQ, 
       g_?NumberQ, Km1_?NumberQ, Km2_?NumberQ, Km3_?NumberQ, NTP0_?NumberQ] := 
  (model[a, b, c, d, f, g, Km1, Km2, Km3, NTP0] = 
     First[MG /. NDSolve[{ MG'[t] == a*DNA*NTP[t]/(Km1 + NTP[t]) - b MG[t],
                           NTP'[t] == -f*a*DNA*NTP[t]/(Km1 + NTP[t]) - 
                           d MG[t] NTP[t]/(Km2 + NTP[t]) - c NTP[t]/(Km3 + NTP[t]), 
                           GFP'[t] == g*d MG[t] NTP[t]/(Km2 + NTP[t]),
                           NTP[0] == NTP0, MG[0] == 0, GFP[0] == 0},
                         {MG, NTP, GFP}, {t, 0, 800}, Method -> StiffnessSwitching]]);

fit = FindFit[ data, {model[a, b, c, d, f, g, Km1, Km2, Km3, NTP0][t], 
                       a > 0, b > 0, c > 0, d > 0, f > 0, g > 0, 
                       Km1 > 1000, Km2 > 1000, Km3 > 1000, NTP0 > 100000}, 
               {{a, 6.8}, {b, 0.012}, {c, 247}, {d, 1.54}, {f, 19.6}, {g, 22.2}, 
                {Km1, 352200}, {Km2, 127882}, {Km3, 5134.5}, {NTP0, 611628}}, t]

where the data looks like: 

data = {{1.65, 111}, {4.65, 141}, {7.65, 130}, {10.65, 247}, {13.65, 301}, 
        {16.65, 395}, {19.65, 444}, {22.65, 652}, ...};

But now I'd like to do it with DNA being an additional variable included in the data like: 

newdata = {{1.65, 10, 111}, {4.65, 10, 141}, {7.65, 10, 130}, ..., {1.65, 5, -4},
           {4.65, 5, 118}, {7.65, 5, 86}, {10.65, 5, 85}, {13.65, 5, 110}, ...};

so that I could fit multiple curves with different values of DNA simultaneously. I imagine that this is something that's possible, but I'm not sure on the syntax. Anyone have any thoughts on this?

------ EDIT --------

so now I've tried to follow the example that bobthechemist gave on the linked page, but I think I'm getting hung up on the syntax:

model[ c_?NumberQ, d_?NumberQ, f_?NumberQ, Km1_?NumberQ, Km2_?NumberQ, Km3_?NumberQ, 
Km4_?NumberQ ][ DNA_?NumberQ, t_?NumberQ] := 
(model[c,d,f, Km1,Km2,Km3,Km4][t,DNA] =  First[MG/.ParametricNDSolve[{
MG'[t,DNA]==a*DNA*NTP[t,DNA]^n/(Km1^n+NTP[t,DNA]^n)b(Km4^n/(Km4^n+NTP[t,DNA]^n))MG[t,DNA],
NTP'[t,DNA]==-a*f*DNA*NTP[t,DNA]^n/(Km1^n+NTP[t,DNA]^n)-d*MG[t,DNA]NTP[t,DNA]^n/(Km2^n+NTP[t,DNA]^n)-c NTP[t,DNA]^n/(Km3^n+NTP[t,DNA]^n),
NTP[0]==NTP0,MG[0]==0}/.{n->1,b->0.012,a->3.5,NTP0->1500000},{MG,NTP},{t,0,800},{DNA},Method->StiffnessSwitching]]);

fit=FindFit[newdata10,{model[c,d,f, Km1,Km2,Km3,Km4][t,DNA],c>0,0<d,0<f,Km1>100000,Km2>100000,Km3>100000,Km4>100000},{{c,91.0400},{d,8.4986},{f,0.000018697},{Km1,1000100},{Km2,5005020},{Km3,5000150},{Km4,7000000}},{t,DNA},Method->"NMinimize"]

gives a whole bunch of errors. perhaps this kind of problem is a bit beyond someone with my limited grasp of Mathematica syntax

------ EDIT 2 --------

a more complete set of data: 

data = {{2.65,5,86}, {5.65,5,85}, {8.65,5,110}, {11.65,5,153}, {14.65,5,187}, {17.65,5,293}, {20.65,5,321}, {23.65,5,320}, {26.65,5,402}, {29.65,5,355}, {32.65,5,593}, {35.65,5,589}, {38.65,5,653}, {41.65,5,687}, {44.65,5,752}, {47.65,5,858}, {50.65,5,882}, {53.65,5,933}, {56.65,5,1033}, {59.65,5,1043}, {62.65,5,1144}, {65.65,5,1178}, {68.65,5,1239}, {71.65,5,1264}, {74.65,5,1317}, {77.65,5,1452}, {80.65,5,1449}, {83.65,5,1465}, {86.65,5,1480}, {89.65,5,1500}, {92.65,5,1529}, {95.65,5,1531}, {98.65,5,1676}, {101.65,5,1626}, {104.65,5,1632}, {107.65,5,1699}, {110.65,5,1560}, {113.65,5,1651}, {116.65,5,1756}, {119.65,5,1767}, {122.65,5,1715}, {125.65,5,1716}, {128.65,5,1715}, {131.65,5,1732}, {134.65,5,1705}, {137.65,5,1740}, {140.65,5,1759}, {143.65,5,1698}, {146.65,5,1653}, {149.65,5,1628}, {152.65,5,1677}, {155.65,5,1711}, {158.65,5,1608}, {161.65,5,1670}, {164.65,5,1481}, {167.65,5,1563}, {170.65,5,1562}, {173.65,5,1588}, {176.65,5,1540}, {179.65,5,1480}, {182.65,5,1462}, {185.65,5,1424}, {188.65,5,1446}, {191.65,5,1412}, {194.65,5,1380}, {197.65,5,1341}, {200.65,5,1338}, {203.65,5,1263}, {206.65,5,1244}, {209.65,5,1237}, {212.65,5,1164}, {215.65,5,1050}, {218.65,5,1109}, {221.65,5,1041}, {224.65,5,1071}, {227.65,5,908}, {230.65,5,940}, {233.65,5,1013}, {236.65,5,913}, {239.65,5,976}, {242.65,5,886}, {245.65,5,847}, {248.65,5,819}, {251.65,5,784}, {254.65,5,818}, {257.65,5,815}, {260.65,5,807}, {263.65,5,704}, {266.65,5,705}, {269.65,5,816}, {272.65,5,758}, {275.65,5,757}, {278.65,5,633}, {281.65,5,708}, {284.65,5,675}, {287.65,5,632}, {290.65,5,617}, {293.65,5,621}, {296.65,5,594}, {299.65,5,558}, {2.65,10,130}, {5.65,10,247}, {8.65,10,301}, {11.65,10,395}, {14.65,10,444}, {17.65,10,652}, {20.65,10,701}, {23.65,10,840}, {26.65,10,922}, {29.65,10,1074}, {32.65,10,1154}, {35.65,10,1209}, {38.65,10,1326}, {41.65,10,1470}, {44.65,10,1628}, {47.65,10,1600}, {50.65,10,1679}, {53.65,10,1759}, {56.65,10,1856}, {59.65,10,1887}, {62.65,10,2057}, {65.65,10,2078}, {68.65,10,2182}, {71.65,10,2128}, {74.65,10,2034}, {77.65,10,2257}, {80.65,10,2337}, {83.65,10,2362}, {86.65,10,2330}, {89.65,10,2423}, {92.65,10,2471}, {95.65,10,2440}, {98.65,10,2388}, {101.65,10,2544}, {104.65,10,2436}, {107.65,10,2538}, {110.65,10,2402}, {113.65,10,2406}, {116.65,10,2423}, {119.65,10,2365}, {122.65,10,2345}, {125.65,10,2391}, {128.65,10,2412}, {131.65,10,2375}, {134.65,10,2309}, {137.65,10,2321}, {140.65,10,2389}, {143.65,10,2212}, {146.65,10,2211}, {149.65,10,2276}, {152.65,10,2188}, {155.65,10,2112}, {158.65,10,2223}, {161.65,10,1980}, {164.65,10,2046}, {167.65,10,2045}, {170.65,10,2022}, {173.65,10,1933}, {176.65,10,1901}, {179.65,10,1925}, {182.65,10,1829}, {185.65,10,1873}, {188.65,10,1840}, {191.65,10,1855}, {194.65,10,1752}, {197.65,10,1682}, {200.65,10,1639}, {203.65,10,1752}, {206.65,10,1784}, {209.65,10,1661}, {212.65,10,1608}, {215.65,10,1563}, {218.65,10,1462}, {221.65,10,1563}, {224.65,10,1543}, {227.65,10,1448}, {230.65,10,1376}, {233.65,10,1384}, {236.65,10,1383}, {239.65,10,1340}, {242.65,10,1263}, {245.65,10,1362}, {248.65,10,1201}, {251.65,10,1206}, {254.65,10,1220}, {257.65,10,1185}, {260.65,10,1164}, {263.65,10,1133}, {266.65,10,1154}, {269.65,10,1115}, {272.65,10,1122}, {275.65,10,1028}, {278.65,10,1049}, {281.65,10,1042}, {284.65,10,960}, {287.65,10,1011}, {290.65,10,940}, {293.65,10,927}, {296.65,10,877}, {299.65,10,888}};

in each triplet of numbers, the first is the time, second is the DNA parameter value, and the third is the value of the function.

dantimatter
  • 51
  • 4
  • 2
    This might be related. – bobthechemist Sep 16 '13 at 22:17
  • Thanks @bobthechemist!

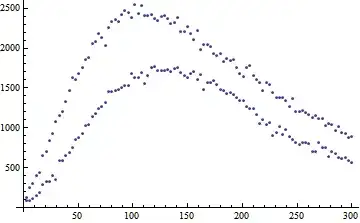
    Although now that I've played with the model a bit more, I've come to realize that my problem has more to do with the structure of the equations. It would seem that there are a extremely large number of local minima, or some other reason why the parameters I get are not very good and the solutions are highly dependent on the starting values of the parameters. :( I'm not sure what could be done about this...

     – dantimatter Sep 19 '13 at 00:50
  • You might be able to look for a least squares solution graphically although the solution I presented there was more of a suggestion for exploration... – bobthechemist Sep 19 '13 at 01:56
  • hi @bobthechemist, i tried just following the example in the page you linked to, just to see what would happen. no luck. i suspect i've committed a number of syntactical errors. my attempt is shown below the 'EDIT' line above. – dantimatter Sep 19 '13 at 22:57
  • Do you have a more complete set of data that can be posted? It would be helpful to have a working sample set even if it is not a complete one. – bobthechemist Sep 19 '13 at 23:47
  • see Edit 2 above for a more complete set of data. it's for two different values for the DNA parameter (5 and 10). first number in the triplet is the time, and the last is the value of MG. thanks @bobthechemist ! – dantimatter Sep 20 '13 at 03:15

2 Answers2

1

Not an answer yet, but a step (hopefully) towards solving the problem.

Plotting the same data set provided gives us:

Mathematica graphics

For the two possible values of DNA. The model contains a whopping 10 adjustable parameters which concerns me a bit, given the general lack of features in the data. I think it is worthwhile to explore how the different adjustable parameters affect the shape of the model output, so that's what I'm doing here with ParametricNDSolveValue. I used lowercase functions just for style purposes, but I think I've copied the code correctly without typos.

eqns = {
   mg'[t] == a dna ntp[t]/(km1 + ntp[t]) - b mg[t],
   ntp'[t] == -f a dna ntp[t]/(km1 + ntp[t]) - 
     d mg[t] ntp[t]/(km2 + ntp[t]) - c ntp[t]/(km3 + ntp[t]),
   gfp'[t] == g d mg[t] ntp[t]/(km2 + ntp[t]),
   ntp[0] == 100000, mg[0] == 0, gfp[0] == 0} /. {dna -> 5}
pfun = ParametricNDSolveValue[
  eqns, {mg, ntp, gfp}, {t, 0, 300}, {a, b, c, d, f, g, km1, km2, 
   km3}]
Manipulate[
 Plot[pfun[a, b, c, d, f, g, km1, km2, km3][[1]][t], {t, 0, 300}],
 {a, 1, 10}, {b, 1, 10}, {c, 1, 10}, {d, 1, 10}, {f, 1, 10}, {g, 1, 
  10}, {km1, 1000, 9999}, {km2, 1000, 9999}, {km3, 1000, 9999}]

Mathematica graphics

I played around with manipulate values, taking a through g to have possible values from 1 to 10 and km1, km2, and km3 to have values from 1000 to 10000. In this example, I fixed ntp = 100000 and dna=5. As you can see, it is hard to get a shape that even remotely matches the dataset. In order to move forward with the model fitting, I think a better set of starting values is going to be needed, unless it is possible to simplify the model to one that has fewer parameters.

bobthechemist
  • 19,693
  • 4
  • 52
  • 138
  • since first posting this i've been able to independently get values for parameters a (a = 3.5) and b (b = 0.012). so these are fixed.

    two additional things that can be done: (1) get rid of the equation for gfp[t] (and thus get rid of the parameter g), since we're not fitting the gfp data here, or (2) fit the additional gfp data i've got and the MG data at the same time.

    since I'm not exactly sure how to fit the gfp and MG data simultaneously, maybe (1) is preferable? if we get rid of a,b, and g, would that help at all?

     – dantimatter Sep 21 '13 at 20:58
  • oh, and NTP0=1500000, also determined through an independent measurement. so if we get rid of the gfp[t] equation the only parameters from the original model that need to be fit are c, d, f, Km1, Km2, and Km3. thanks for everything, @bobthechemist! – dantimatter Sep 22 '13 at 17:10
  • @dantimatter, you should be able to alter the code above to delete references to gfp and insert values for a, b and NTP0. When I do this, I still get a solution that doesn't look anything like the experimental data. Possible next steps include: (a) ensuring the model is appropriate and correct; (b) continuing to find parameter values independently; (c) Adjust the Manipulate to see if the model does give a reasonable fit with some range of parameters. Since I don't know this data, model or experiment, it's hard to provide more constructive feedback. Sorry. – bobthechemist Sep 22 '13 at 17:46
  • thanks for all your help, @bobthechemist. :) i'll hack at it a bit more and post here again if there's anything new to add to the story.
    eventually the associated work will be published and when that happens i'd like to acknowledge your help on this. if you're interested, google dantimatter, find my contact info, and send me a note with your information. thanks again.     – dantimatter Sep 23 '13 at 01:46
1

So it turns out that my institution has a certain amount of Mathematica technical support included in their license. I posed this question to the good people at Wolfram and this was their response:

"I've attached a notebook containing examples of how you might successfully use FindFit with your parametric differential equation system.

The notebook doesn't contain the results of the FindFit evaluations, as they seemed to be taking a bit of time to evaluate. However, the syntax and usage of all expressions in the notebook is correct as far as I have tested and should give you a fit to your model."

The contents of the notebook are below.

ClearAll[DNA];
solutions =
 ParametricNDSolve[
   {Derivative[1, 0][MG][t, DNA] == 
     a*DNA*NTP[t, DNA]/(Km1 + NTP[t, DNA]) - b*MG[t, DNA],
    Derivative[1, 0][NTP][t, DNA] ==
     -f*a*DNA*NTP[t, DNA]/(Km1 + NTP[t, DNA]) - 
 d*MG[t, DNA] NTP[t, DNA]/(Km2 + NTP[t, DNA]) - 
 c*NTP[t, DNA]/(Km3 + NTP[t, DNA]),
    Derivative[1, 0][GFP][t, DNA] == 
g*d*MG[t, DNA] NTP[t, DNA]/(Km2 + NTP[t, DNA]),
    NTP[0, DNA] == NTP0,
    MG[0, DNA] == 0,
    GFP[0, DNA] == 0},
   {MG, NTP, GFP},
   {t, 0, 800},
   {DNA, 5, 10},(* 
   chosen as example domain *)
   {a, b, c, d, f, g, Km1, Km2, Km3, 
    NTP0},
   Method -> "StiffnessSwitching"
   ]

ClearAll[model];
model = MG /. solutions;

parameters = {a, b, c, d, f, g, Km1, Km2, Km3, NTP0};

startingValues = {6.8`, 0.012`, 247, 1.54`, 19.6`, 22.2`, 352200, 127882, 
   5134.5`, 611628};

(* quick test *)
model @@ startingValues
%[100, 7]

fit =
 FindFit[
  data,
  {model[a, b, c, d, f, g, Km1, Km2, Km3, NTP0][t, DNA],
   {a > 0, b > 0, c > 0,
    d > 0, f > 0, g > 0,
    Km1 > 1000, Km2 > 1000, Km3 > 1000,
    NTP0 > 100000}},
  Thread@{parameters, startingValues},
  {t, DNA}
  ]
dantimatter
  • 51
  • 4