How to find the non-differentiable point(s) of a given continuous function?

Question

For example, the non-differentiable point of the function $f(x)=|x|$ is at $x=0$.
How to find the non-differentiable points of a continuous function that is defined numerically?

Answer 1

If we define f[x] e.g. like this:

f[x_] := Abs[x]

the following returns interesting points:

Reduce[ 
    Limit[(f[x + h] - f[x])/h, h -> 0, Assumptions -> x ∈ Reals, Direction -> -1] != 
    Limit[(f[x + h] - f[x])/h, h -> 0, Assumptions -> x ∈ Reals, Direction -> 1],  x]

x == 0

Let's try another function defined with Piecewise, e.g.

g[x_] := Piecewise[{{x^2, x < 0}, {0, x == 0}, {x, 1 > x > 0}, 
                    {1, 2 >= x >= 1}, {Cos[x - 2] + x - 2, x > 2}}]

then we needn't use Assumptions in Limit:

Reduce[ Limit[ (g[x + h] - g[x])/h, h -> 0, Direction -> -1] != 
        Limit[ (g[x + h] - g[x])/h, h -> 0, Direction -> 1], x]

 x == 0 || x == 1 || x == 2

pts = {x, g[x]} /. {ToRules[%]};

Plot[ g[x], {x, -5/4, 3}, PlotStyle -> Thick, 
      Epilog -> {Red, PointSize[0.023], Point[pts]}]

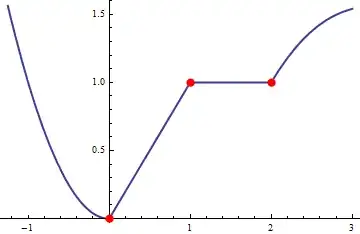
One should be careful when working with Piecewise since Reduce may produce errors when weak inequalities (LessEqual) are involved. For this reason we added {0, x == 0} in the definition of the function g.

Answer 2

Here is an approach that you can use for numerical functions that at least have a left and right derivative. If such a function isn't differentiable in a point that is equivalent to the left and right derivatives being unequal, so look at the left and right finite difference approximation of the derivative, and see where they disagree.

rightd[f_, h_, x_] := (f[x + h] - f[x])/h
leftd[f_, h_, x_] := (f[x] - f[x - h])/h

f[x_?NumericQ] := If[x < .13, 0 , x - .13 ]

Plot[Abs[leftd[f, 0.1, x] - rightd[f, 0.1, x]], {x,-1,1}, PlotRange->All]

Using this you can use some numerical maximization on Abs[leftd[f, h, x] - rightd[f, h, x]], perhaps with successively smaller h to avoid false positives.

Answer 3

Some things change to better since 12.2

FunctionDiscontinuities[D[RealAbs[x], x], x]

RealAbs[x] == 0

FunctionDiscontinuities[CantorStaircase'[x], x]

Falseand a warning "FunctionDiscontinuities::unkds: Warning: The set of discontinuities may be incomplete due to missing domain and discontinuity information for some of the functions involved."

and since 10.0

FunctionDomain[RealAbs'[x], x, Reals]

x < 0 || x > 0