Filling Fill incomplete in ListLinePlot

Question

data = {{0., 0., 0}, {0.12, 0.04, 2}, {0.24, 0.08, 4}, {0.36, 0.11, 
    6}, {0.47, 0.15, 8}, {0.59, 0.19, 10}, {0.71, 0.23, 12}, {0.83, 
    0.26, 14}, {0.95, 0.3, 16}, {1.07, 0.34, 18}, {1.21, 0.38, 
    20}, {1.38, 0.41, 22}, {1.78, 0.45, 24}, {2.84, 0.49, 26}, {3.45, 
    0.52, 28}, {3.88, 0.56, 30}, {4.33, 0.6, 32}, {4.79, 0.64, 
    34}, {5.25, 0.64, 36}, {5.89, 0.3, 38}, {6.16, 0.68, 40}, {6.51, 
    0.84, 42}, {6.89, 0.98, 44}, {7.27, 1.14, 46}, {7.67, 1.39, 
    48}, {8.07, 1.95, 50}, {8.47, 5.3, 52}, {8.89, 5.82, 54}, {9.3, 
    6.14, 56}, {9.71, 6.48, 58}, {10.11, 6.9, 60}, {10.52, 7.56, 
    62}, {10.92, 8.18, 64}, {11.32, 8.55, 66}, {11.72, 8.86, 
    68}, {12.13, 9.16, 70}, {12.53, 9.46, 72}, {12.93, 9.77, 
    74}, {13.33, 10.07, 76}, {13.73, 10.38, 78}};

ListLinePlot[data[[;; , {#, 3}]] & /@ {1, 2}, Filling -> {1 -> {2}}, Frame -> 1]

My code gives this

enter image description here

but I want it look like this

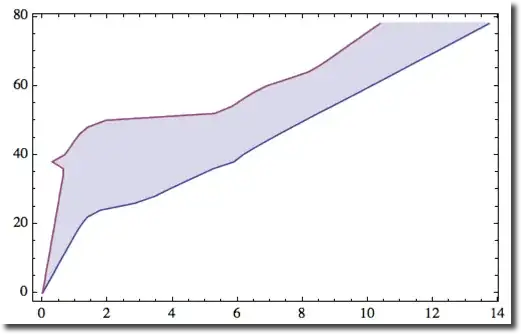
enter image description here

You can use Filling -> {1 -> Top, 2 -> {Top, White}} for this particular plot — panda-34, Sep 24 '13 at 08:06

score 10 · Accepted Answer · edited Jan 10 '14 at 09:52

10

Reverse points around y=x axis (flip y-x coordintaes) to get correct filling
But now you plot is flipped - so flip again around y=x with GeometricTransformation

Here it is:

pl = ListLinePlot[(Reverse /@ data[[All, {#, 3}]]) & /@ {1, 2}, Filling -> {1 -> {2}}];
Graphics[GeometricTransformation[pl[[1, 2]], ReflectionTransform[{-1, 1}]], Frame -> True, 
 AspectRatio -> 1/GoldenRatio]

enter image description here

edited Jan 10 '14 at 09:52

Mr.Wizard

271,378
34
587
1,371

answered Sep 24 '13 at 05:46

Vitaliy Kaurov

73,078
9
204
355

+1 ... there is a german saying: "Von hinten durch die Brust ins Auge" which kinda fits here :-) – Yves Klett Sep 24 '13 at 11:52
@YvesKlett Yep, "From behind through the chest into the eye" ;-) – Vitaliy Kaurov Sep 24 '13 at 14:57
In version 7 I need Normal[pl][[1]] in place of pl[[1, 2]] for this to work. (+1) – Mr.Wizard Jan 10 '14 at 09:51
We have a similar saying: "Around your ass into your pocket." – shrx Jan 10 '14 at 10:54

m_goldberg · Answer 2 · 2013-09-24T11:47:34.327

I like the solution panda-34 gave in a comment on the question. It is simple and gets the job done

ListLinePlot[data[[;; , {#, 3}]] & /@ {1, 2},
  Filling -> {{1 -> Top}, {2 -> {Top, White}}},
  Frame -> True]

However, if there is some reason why it would be undesirable to have the upper left region of the plot rectangle filled with opaque white, you can get the results you want by appending a data point to the data for the upper curve that extends it to the far right of the plot rectangle but puts it outside the plot range.

Module[{d1, d2},
  {d1, d2} = data[[;; , {#, 3}]] & /@ {1, 2};
  AppendTo[d2, {data[[-1, 1]], 2 + data[[-1, -1]]}];
  ListLinePlot[{d1, d2},
    PlotRange -> {0, data[[-1, -1]]},
    PlotRangePadding -> {.25, 2},
    Filling -> {1 -> {2}},
    Frame -> True]]

Both of the above expressions produce the desired plot when evaluated:

Filling Fill incomplete in ListLinePlot

2 Answers2

Linked