Highlighting a single Period of a Trig Plot

Question

How do I highlight a single period of a trig function say by using color and/or thickness when the graph itself extends further than just a single period? Thanks...Gregory Lane

Answer 1

Plot[Sin[x], {x, -4 Pi, 4 Pi}, Mesh -> {{0, 2 Pi}}, 
 MeshShading -> {ColorData[1][1], Red}]

---

Update

[@belisarius pointed out that another answer shows the built-in, but undocumented, function Period`PeriodicFunctionPeriod that returns the period of a periodic function with exact coefficients.]

If you'd like more general functionality, one can write a function to get the period and another to highlight a period from an arbitrary starting point. The pattern in getPeriod parses the typical affine transformations of trigonometric graphs studied in school.

ClearAll[highlightPeriod, getPeriod];
SetAttributes[highlightPeriod, HoldAll];
SetAttributes[getPeriod, HoldAll];

getPeriod[f_, var_] := 
  Periodic`PeriodicFunctionPeriod[Rationalize[f, 0], var];

highlightPeriod[f_, dom_, x0_: 0., opts : OptionsPattern[Plot]] :=
  Block @@
   Join[
    Hold[{dom}] /. {x_, __} :> x,
    Hold[
     Plot[f, dom, Mesh -> {{x0, x0 + getPeriod[f, First@dom]}}, 
      MeshShading -> (OptionValue[MeshShading] /. 
         None -> {ColorData[1][1], Red}), opts]
     ]
    ];

The real key is the two lines of the Plot command. The function definition could consist of just these two lines, but there's a risk. The use of Block is to keep the function and variable in the domain dom from evaluating before being passed to Plot. Without this, if x has been set to a numerical value, then its value and not the symbol would be passed to Plot, which would not work since a number cannot serve as a variable.

Calling highlightPeriod is like calling Plot, except there is an option third argument x0 that specifies the starting point of the highlighted period.

Examples:

ex1 = highlightPeriod[Cot[x/2], {x, -4 Pi, 4 Pi}];
ex2 = highlightPeriod[Cot[x/2], {x, -4 Pi, 4 Pi}, Pi,
   MeshShading -> {Purple, Orange},  (* change color *)
   MeshStyle -> None,                (* removes mesh dots *)
   PlotStyle -> Thick];
ex3 = highlightPeriod[2 Cos[1.2 x + 0.5] - 0.7, {x, -4 Pi, 4 Pi}];
ex4 = With[{f = 2 Cos[1.2 x + 0.5] - 0.7},
   highlightPeriod[f, {x, -4 Pi, 4 Pi},
    x /. FindRoot[f, {x, 0.}]]       (* start at a zero of f *)
   ];

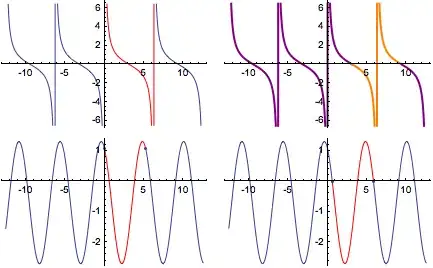
GraphicsGrid@{
  {ex1, ex2},
  {ex3, ex4}}

---

The old getPeriod, for reference:

getPeriod[Sin|Cos|Sec|Csc]:=2Pi;
getPeriod[Tan|Cot]:=Pi;
getPeriod[(amp_:1.) f_[(a_:1.) \
x_Symbol+b_:0]+vshift_:0.]/;NumericQ[a]:=getPeriod[f]/a;

Answer 2

Here is one way:

Show[Plot[Sin[x], {x, 0, 6 Pi}], 
 Plot[Sin[x], {x, 0, 2 Pi}, 
  PlotStyle -> Directive[Red, Thickness[0.01]]]]

If you want to add interactivity, you can translate the red cycle to the right one cycle (or whatever you choose):

Manipulate[
 Show[Plot[Sin[x], {x, 0, 6 Pi}], 
  Plot[Sin[x - j], {x, j, 2 Pi + j}, 
   PlotStyle -> Directive[Red, Thickness[0.01]]]], {j, 0, 2 Pi}]