Composition: how to make a day and night world map?

Question

Given the following world images:

night = Import["http://eoimages.gsfc.nasa.gov/images/imagerecords/55000/55167/earth_lights_lrg.jpg"]
day = Import["http://eoimages.gsfc.nasa.gov/images/imagerecords/57000/57752/land_shallow_topo_2048.tif"]

how would you use Mathematica to create an accurate “day and night map” (examples here and there) of the Earth for a given date and time?

Answer 1

Let me first name your maps correctly (you switched night and day maps):

night= Import["http://eoimages.gsfc.nasa.gov/images/imagerecords/55000/55167/earth_lights_lrg.jpg"];
day= Import["http://eoimages.gsfc.nasa.gov/images/imagerecords/57000/57752/land_shallow_topo_2048.tif"];

The images have different sizes:

ImageDimensions[day]

(*
==> {2048, 1024}
*)

ImageDimensions[night]

(*
==> {2400, 1200}
*)

so, I rescale the night image. Artefacts (if any) will probably be less visible there.

night = ImageResize[night, ImageDimensions[day]];

Now, for the calculation of the mask we don't need to use external sources. AstronomicalData will do:

mask =
 Rasterize[
  RegionPlot[
   AstronomicalData["Sun", {"Altitude", {2012, 6, 21}, {lat, long}}] <
     0, {long, -180, 180}, {lat, -90, 90}, Frame -> None, 
   PlotRange -> Full, PlotStyle -> Black, PlotRangePadding -> 0, 
   AspectRatio -> (#2/#1 & @@ ImageDimensions[day])],
  ImageSize -> ImageDimensions[day]
  ]

Then, stealing the ImageCompose idea from Yu-Sung:

pl=ImageCompose[night, SetAlphaChannel[day, mask]]

Borrowing and adapting some code from the Texture doc page:

Show[
 Graphics3D[{White, Tube[{{0, 0, -1.4}, {0, 0, 1.4}}, .04]}],
 SphericalPlot3D[1 , {u, 0, Pi}, {v, 0, 2 Pi}, Mesh -> None, 
  TextureCoordinateFunction -> ({#5, 1 - #4} &), 
  PlotStyle -> Texture[Show[pl, ImageSize -> 1000]], 
  Lighting -> "Neutral", Axes -> False, RotationAction -> "Clip"], 
 Lighting -> "Neutral", Boxed -> False, 
 Method -> {"ShrinkWrap" -> True}
]

Answer 2

Yes, the basic idea is here: Demonstration: Day and Night World Clock

Now, to use the images, create an alpha channel using the computed the day-night curve--called "terminator" curve (rasterize it in grayscale), and compose two images using ImageCompose with the generated alpha channels (SetAlphaChannel to the second image).

Try the following code:

a = Image[ConstantArray[{255, 0, 0}, {200, 300}]];
b = Image[ConstantArray[{0, 255, 0}, {200, 300}]];

(* This is just a made-up mask. Don't mind the Plot[] part *)
mask = Rasterize[
  Plot[Sin[x], {x, -Pi/2, 3 Pi/2}, PlotRangePadding->0,
    Filling->-1, FillingStyle->Black, Frame->False, 
    Axes->False, ImageSize->{300, 200}, AspectRatio->2/3],
  "Image", ColorSpace->"GrayScale"];

ImageCompose[a, SetAlphaChannel[b, mask]]

You should get an image with green and red mixed as below. Now you can replace a and b with your day and night textures.

I have to tell you that although the code there computes pretty close approximation of the actual terminator curve, it is not exact. To compute it accurately (or based on actual data), see: NOAA: Day Night Terminator

The following code and output is for the actual images (again the mask is fake):

day = ImageResize[day, {2048, 1024}]; (* Match the dimensions *)

mask = Rasterize[
   Plot[Sin[x], {x, -Pi/2, 3 Pi/2}, PlotRangePadding -> 0, 
    Filling -> -1, FillingStyle -> Black, Frame -> False, 
    Axes -> False, ImageSize -> {2048, 1024}, 
    AspectRatio -> 1024/2048], "Image", ColorSpace -> "GrayScale"];

ImageCompose[night, SetAlphaChannel[day, mask]]

Answer 3

Since version 10.0, the functions DayHemisphere[], NightHemisphere[], and DayNightTerminator[] are now built-in, and can be used with GeoGraphics[]. These three can either take a specified date, and will otherwise default to Now. One can now do things like this:

GeoGraphics[{GeoStyling[GrayLevel[0, 2/3]], NightHemisphere[]}, 
            GeoBackground -> GeoStyling["Satellite"], GeoProjection -> "Equirectangular",
            GeoRange -> "World"]

which can then be used as a suitable Texture[] if wanted.

Answer 4

As Sjoerd shows, AstronomicalData[] can be used to determine the altitude of the sun. However, if you do not need too much accuracy, such as in this application, you can use a low-accuracy method for computing the altitude. Most of the formulae I will be using are from (of course) Jean Meeus's Astronomical Algorithms.

Some auxiliary routines will be needed. First, one for computing the Julian Day number:

Options[jd] = {"Calendar" -> "Gregorian"};

jd[{yr_Integer, mo_Integer, da_?NumericQ, rest___}, opts : OptionsPattern[]] := 
  Module[{y = yr, m = mo, h}, If[m < 3, y--; m += 12];
         h = Switch[OptionValue["Calendar"],
                    "Gregorian", (Quotient[#, 4] - # + 2) &[Quotient[y, 100]],
                    "Julian", 0,
                    _, Return[$Failed]];
         Floor[365.25 y] + Floor[30.6001 (m + 1)] + da +
         FromDMS[PadRight[{rest}, 3]]/24 + 1720994.5 + h]

jd[opts : OptionsPattern[]] := jd[DateList[], opts]

Here's a method for computing the Greenwich Mean Sidereal Time:

GMST[{yr_Integer, mo_Integer, da_?NumericQ, rest___}, opts : OptionsPattern[]] := 
    Mod[6.697374558 + 0.06570982441908 (jd[{yr, mo, da}, opts] - 2.451545*^6) +
    1.00273790935 FromDMS[PadRight[{rest}, 3]] + 0.000026 ((jd[{yr, mo, da, rest}, opts] -
    2.451545*^6)/36525)^2, 24]

GMST[opts : OptionsPattern[]] := GMST[DateList[], opts]

Finally, here's the low-accuracy method for computing the solar altitude:

solarAltitude[date_List, {ϕ_, λ_}] := 
 Module[{t, ℳ☉, ℯ, s, ℰ, v, Ω, ℒ0, Λ, ε, α, δ, ℋ},

  t = (jd[date] - 2451545)/36525;

  (* ℳ☉ - mean solar anomaly *)
  ℳ☉ = Mod[(1.28710479305*^6 + t (1.295965810481*^8 + t (-0.5532 + t (1.36*^-4 -
            1.149*^-5 t))))/3600, 360] °;

  (* ℯ - eccentricity of Earth's orbit *)
  ℯ = 0.0167086342 + t (-0.004203654 + t (-0.00126734 +
      t (1.444*^-4 + t (-2.*^-6 + 3.*^-5 t))));

  (* ℰ - eccentric anomaly; approximate solution of Kepler's equation *)
  s = Sin[ℳ☉]; ℰ = ℳ☉ + ℯ s/(s - Sin[ℳ☉ + ℯ] + 1);

  (* v - true anomaly *)
  v = 2 ArcTan[Sqrt[(1 + ℯ)/(1 - ℯ)] Tan[ℰ/2]]/°;

  (* ℒ0 - geometric mean longitude *)
  ℒ0 = (280.46645 + t (36000.76983 + 3.032*^-4 t));

  (* Ω - Meeus's correction for apparent angles *)
  Ω = (125.04 - 1934.136 t) °;

  (* Λ - solar longitude, plus correction for apparent position *)
  Λ = Mod[v + ℒ0 - ℳ☉/°, 360] ° - (0.00569 + 0.00478 Sin[Ω]) °;

  (* ε - mean obliquity of the ecliptic, plus correction for apparent position *)
  ε = (84381.406 + t (-46.836769 + t (-1.831*^-4 + t (0.0020034 +
      t (-5.76*^-7 - 4.34*^-8 t))))) °/3600 + 0.00256 Cos[Ω] °;

  (* α - right ascension, δ - declination *)
  {α, δ} = {ArcTan[Cos[Λ], Sin[Λ] Cos[ε]]/(15 °), ArcSin[Sin[ε] Sin[Λ]]};

  (* ℋ - hour angle *)
  ℋ = 15 ° Mod[FromDMS[GMST[date]] + λ/15 - α, 24];

  ArcSin[Sin[δ] Sin[ϕ °] + Cos[δ] Cos[ϕ °] Cos[ℋ]]/°]

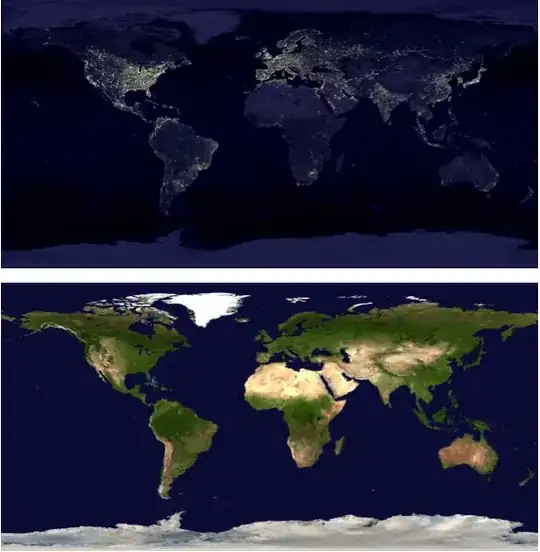
A few nice maps:

earthDay = Import["https://i.stack.imgur.com/KLrc8.jpg"];
earthNight = Import["https://i.stack.imgur.com/mCJik.jpg"];

Finally, the routine for making a day/night map:

Options[DayAndNightMap] = {Sphere -> False, TimeZone :> $TimeZone};

DayAndNightMap[date_List, opts : OptionsPattern[]] := 
   Module[{h = OptionValue[TimeZone], terminator, dayAndNight},
          terminator = Binarize[
          RegionPlot[Positive[solarAltitude[DatePlus[date, {-h, "Hour"}], {ϕ, λ}]],
                     {λ, -180, 180}, {ϕ, -90, 90}, AspectRatio -> Automatic, 
                     BoundaryStyle -> None, Frame -> False, ImagePadding -> None, 
                     ImageSize -> {2048, 1024}, PlotPoints -> 45, 
                     PlotRangePadding -> None, PlotStyle -> Black]];

          dayAndNight = RemoveAlphaChannel[ImageCompose[earthDay,
                        SetAlphaChannel[earthNight, terminator]]];

          If[TrueQ[OptionValue[Sphere]],
             ParametricPlot3D[{Cos[λ] Sin[ϕ], Sin[λ] Sin[ϕ], Cos[ϕ]},
                              {λ, -π, π}, {ϕ, 0, π}, Axes -> None, Boxed -> False,
                              Lighting -> "Neutral", Mesh -> None, PlotPoints -> 55,
                              PlotStyle -> Texture[dayAndNight], RotationAction -> "Clip",
                              TextureCoordinateFunction -> ({#4, 1 - #5} &)],
             dayAndNight]]

DayAndNightMap[opts : OptionsPattern[]] := DayAndNightMap[DateList[], opts]

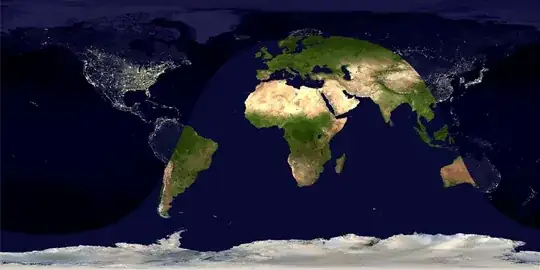
I guess an example is in order at this point:

DayAndNightMap[{2013, 5, 21, 15, 30, 0}, TimeZone -> 0]

For the kids who prefer actual globes:

DayAndNightMap[{2013, 5, 21, 15, 30, 0}, Sphere -> True, TimeZone -> 0]