How to optimize computing a product?

Question

Problem description

Write a function to caculate the formula

formula

My solutions

Solution 1:

  expBreak[n_Integer] := Which[
  n == 1, Sqrt[2], 
  n >= 2, (Product[
            ((2^(n - 1) + 2 i + 1)^2 - 1)/
             (2^(n - 1) + 2 i + 1)^2, {i, 0, 2^(n - 2) - 1}])^(1/2^n)]
  expHalf[n_Integer ] := Product[expBreak[i], {i, 1, n}]

Timing @ (expHalf[20] 2 // N)

{113.896 second, 2.71828}

Solution 2:

  numeratorList[n_] :=
    (Most@Riffle[Table[2 i, {i, 1, 2^(n - 1)}], 
      Table[2 i, {i, 1, 2^(n - 1)}]])[[2^(n - 1) ;; 2^n - 1]]
  denominatorList[n_] :=
    (Rest@Riffle[Table[2 i - 1, {i, 1, 2^n}], 
      Table[2 i - 1, {i, 1, 2^n}]])[[2^(n - 1) ;; 2^n - 1]]
  exphalf[n_] := 
    Product[(Times @@ numeratorList[i]/Times @@ denominatorList[i])^(1/2^
             i), {i, 1, n}]

Timing @ (exphalf[20] 2 // N)

{95.659 second, 2.71828}

So my question is how to revise it and make it more efficient?

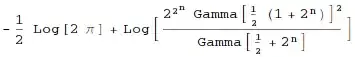
There is a typo, exp is a function. e is what you are calculating. — Kuba, Oct 03 '13 at 06:08
Possible duplicate http://mathematica.stackexchange.com/q/26732/973 — Fred Daniel Kline, Oct 03 '13 at 10:17

ybeltukov · Accepted Answer · 2013-10-03T14:18:50.377

Update: ~10000x speedup with Gamma of real numbers.

Update2: There are a simple analytic formula for the finite product (see e7)

You can rewrite these products with FactorialPower

e3[m_] := Sqrt[2] Product[(FactorialPower[2^(n + 1), 2^(n - 1), 2]/(
    Sqrt[2] N@FactorialPower[2^(n + 1) - 1, 2^(n - 1), 2]))^2^-n, {n, 1, m - 1}]

Or take the logarithm and simplify

FullSimplify[
 FunctionExpand@
  Log[FactorialPower[2^(n + 1), 2^(n - 1), 2]/(
   Sqrt[2] FactorialPower[2^(n + 1) - 1, 2^(n - 1), 2])], 
 Assumptions :> n > 0]

enter image description here

e4[m_] := Sqrt[2] Exp@Sum[Log[2] + 2.0^-n (2 LogGamma[1/2 (1 + 2.0^n)] - LogGamma[1/2+2.0^n]
    - 1/2 Log[2 Pi]), {n, 1, m - 1}]

Timings are considerably better then in the answer of Kuba

2 e[20] // AbsoluteTiming (* Kuba *)
2 e3[20] // AbsoluteTiming
2 e4[20] // AbsoluteTiming

{4.826520, 2.71828}
{0.722181, 2.71828}
{0.000551, 2.71828}  (* !!! *)

Further optimizations: you can easily get rid of the summation

e5[m_] := Sqrt[2] Exp[(m - 1) Log[2] - (1 - 2^(1 - m)) 1/2 Log[2 Pi] + 
    LogGamma[1.5] - 2.0^(1 - m) LogGamma[1/2 + 2^(m - 1)]]

e6[m_] := 
 2.0^(m - 0.5) (2 Pi)^(-(1 - 2^(1 - m))/2) Gamma[1.5]/
   Gamma[1/2 + 2^(m - 1)]^2.0^(1 - m)

e7[m_] := 2.0^(-2.0^-m + m) (Gamma[2.0^(m - 1)]/Gamma[2.0^m])^2.0^(1 - m)

2 e5[20] // AbsoluteTiming
2 e6[20] // AbsoluteTiming
2 e7[20] // AbsoluteTiming

{0.000114, 2.71828}
{0.000160, 2.71828}
{0.000140, 2.71828}

Validation:

e[2] == e3[2] == e4[2] == e5[2] == e6[2] == e7[2]

True

Kuba · Answer 2 · 2013-10-03T07:07:09.467

You will get faster code if you apply N earlier. I will not improve your code, just show slightly different approach with the N earlier:

num2[1] = 2;
num2[n_] := (2^(n - 1)) (2^n) Times @@ (Range[2^(n - 1) + 2, 2^n - 2, 2]^2)


den2[1] = 1;
den2[n_] := Times @@ (Range[2^(n - 1) + 1, 2^n - 1, 2]^2)

e[n_] := Module[{i = 0}, Times @@ (N[N[(num2[#]/den2[#])]^(1/2^(++i))] & /@ Range[n])]

e[20] 2 // AbsoluteTiming

{13.437500, 2.71828}

Try this with yours and compare results.

Edit more compact way for final function. But it seems only more compact, not faster:

e2[n_] := Times @@ (Array[N[N[(num2[#]/den2[#])]^(1/2^(#))] &, n])

How to optimize computing a product?

2 Answers2