How I can make a menu with different graphs with modifiable parameters?

Question

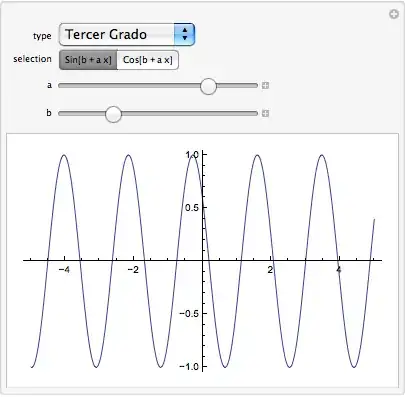
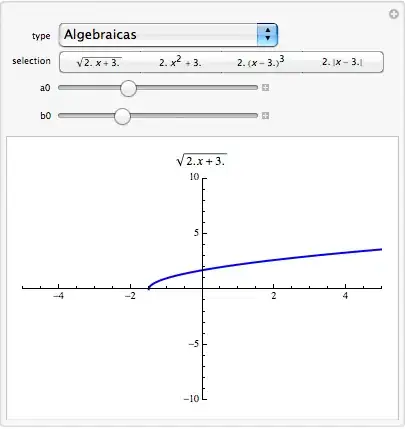
I want a user friendly window in which to have a menu where you can choose the chart you want to display, in which you can move parameters in order to note the width or height of the chart, but I try to declare a function which call control so that using TraditionalForm displayed as the user can understand it, but it is no longer displayed graph. My question is: How I can do to have a function declared prior to Manipulate plot and also will allow me to move the parameters?

  a = "Algebraicas";
  b = "Trigonometricas";
  c = "Tercer Grado";
  y = w + 1;
  Module[{myPlot}, myPlot[f_] := Plot[f[x], {x, -5, 5}];
        Manipulate[
        myPlot@selection,
        {x, {a, b, c}, ControlType -> PopupMenu},
            {{selection, None}, selChoice, ControlType -> SetterBar},        
        {selChoice, Which[
                  x == a, {Sqrt[y] -> TraditionalForm[Sqrt[y]] &, #^2 &},
                  x == b, {#^3 &, Abs@# &},
                  x == c, {Sin, Cos}]}, None}]]

but I need to do is you can move the graph parameters, such as:

Manipulate[Plot[Sin[a x + b], {x, 0, 6}], {a, 1, 4}, {b, 0, 10}]

Now I want to have a label on each graph which is observed as the values are updated manipulate the slide, this is the code that I have.

 Clear[a, b, c];
 types = {"Algebraicas", "Logaritmicas y exponenciales", 
  "Trigonometricas", "Trigonometricas Inversas", "Hiperbolicas", 
  "Hiperbólicas Inversas"};

  Manipulate[
     Plot[
         selection /. {a -> a0, b -> b0}, {x, -5, 5}, 
         PlotRange -> {{-5, 5}, {-10, 10}}, PlotStyle -> {Blue, Thick}, 
         PlotLabel -> selection],
 {type, types, ControlType -> PopupMenu},
     {selection, Dynamic[type /. 
      Thread[types -> {{Sqrt[a x + b] -> TraditionalForm[Sqrt[a x + b]],
        a x^2 + b, a (x - b)^3, a Abs[x - b]}, {Log[10, 1000], 
       Log[E, x], Log[1000.]}, {Sin[a x + b], Cos[a x + b], 
       Tan[a x + b]}, {Cot[a x + b], Csc[a x + b], 
       Sec[a x + b]}, {"a"}, {"b"}}]],
       ControlType -> SetterBar},
       {{a0, 1, a}, 1, 4}, {{b0, 0, b}, 0, 10}]

This is the new code.

   Clear[Seleccion, tipos, Tipo, selecciones, funciones, a, b, c, d, a0, \
   b0, c0, d0]
   tipos = {"Algebraicas", "Logaritmicas y exponenciales", 
   "Trigonometricas", "Trigonometricas Inversas", "Hiperbolicas", 
   "Hiperbólicas Inversas"};
   funciones = {{c ( x/d + a) + b, c Sqrt[ x/d + a] + b, 
   c ( x/d + a)^2 + b, c (x/d + a)^3 + b, c Abs[x/d + a] + b, 
   c/(x/d + a) + b, c/(x/d + a)^2 + b}, {c Log[E, x/d + a], 
   c Log[2, x/d + a] + b, c Log[(1/2), x/d + a] + b, 
   c Exp[x/d + a] + b, c 2^(x/d + a) + b, 
   c (1/2)^(x/d + a) + b}, {c Sin[x/d + a] + b, c Cos[x/d + a] + b, 
   c Tan[ x/d + a] + b, c Cot[x/d + a] + b, c Csc[x/d + a] + b, 
   c Sec[ x/d + a] + b}, {c ArcSin[ x/d + a] + b, 
   c ArcCos[ x/d + a] + b, c ArcTan[ x/d + a] + b, 
   c ArcCot[x/d + a] + b, c ArcCsc[x/d + a] + b, 
   c ArcSec[ x/d + a] + b}, {c Sinh[x/d + a] + b, 
   c Cosh[x/d + a] + b, c Tanh[ x/d + a] + b, c Coth[x/d + a] + b, 
   c Csch[x/d + a] + b, 
   c Sech[ x/d + a] + b}, {c ArcSinh[ x/d + a] + b, 
   c ArcCosh[ x/d + a] + b, c ArcTanh[ x/d + a] + b, 
   c ArcCoth[x/d + a] + b, c ArcCsch[x/d + a] + b, 
   c ArcSech[ x/d + a] + b}};

   Manipulate[Seleccion = tipos /. Thread[tipos -> funciones[[All, 1]]];
   Dynamic@Plot[
   Seleccion /. {a -> a0, b -> b0, c -> c0, d -> d0}, {x, -5, 5}, 
   PlotRange -> {{-5, 5}, {-10, 10}}, PlotStyle -> {Orange, Thick}, 
   PlotLabel -> 
   Style [Framed[
   Pane[TraditionalForm[
    Seleccion /. {a -> a0, b -> b0, c -> c0, d -> d0}, 
    3], {Automatic, 40}]], White, Background -> Lighter[Gray]], 
   AxesLabel -> {Style[x, Large, Bold, Blue], 
   Style[y, Large, Bold, Blue]}, 
   LabelStyle -> Directive[Black, Bold], ImageSize -> 540], {Tipo, 
   tipos, ControlType -> PopupMenu}, {Seleccion, 
   Dynamic[Tipo /. 
   Thread[tipos -> 
    With[{selecciones = Map[# &, funciones, {2}]}, selecciones]]], 
    ControlType -> SetterBar}, {{a0, 0, "a"}, -3, 3}, {{b0, 0, "b"}, -3,
    3}, {{c0, 1, "c"}, -3, 3}, {{d0, 1, "d"}, -3, 3}]

@Kuba: see also here: http://mathematica.stackexchange.com/questions/33081/how-do-you-put-a-plot-inside-a-popupmenu-that-is-inside-another-popupmenu/33084#33084 — Pinguin Dirk, Oct 03 '13 at 18:09

score 2 · Accepted Answer · edited Apr 13 '17 at 12:55

Here's a guess at what you're after, although I think b and c are switched.

a = "Algebraicas";
b = "Trigonometricas";
c = "Tercer Grado";
y = w + 1;
Manipulate[
 Plot[selection, {x, -5, 5}],
 {type, {a, b, c}, ControlType -> PopupMenu},
 {selection, 
  Dynamic[type /. {a -> {Sqrt[x] -> TraditionalForm[Sqrt[x]], x^2}, 
                   b -> {x^3, Abs@x}, c -> {Sin[x], Cos[x]}}], 
  ControlType -> SetterBar}
 ]

Mathematica graphics

If you make the list for selection Dynamic, it will automatically reset the SetterBar when a different type is chosen.

Update

Making plots depend on parameters is covered here: How are parameters evaluated for a Plot in Manipulate

For example, here is a common solution using ReplaceAll:

Clear[a, b, c];
types = {"Algebraicas", "Trigonometricas", "Tercer Grado"};

Manipulate[
 Plot[selection /. {a -> a0, b -> b0}, {x, -5, 5}],

 {type, types, ControlType -> PopupMenu}, {selection, 
  Dynamic[type /. 
    Thread[types -> {{Sqrt[a x + b] -> TraditionalForm[Sqrt[a x + b]],
         a x^2 + b}, {a (x - b)^3, a Abs[x - b]}, {Sin[a x + b], 
        Cos[a x + b]}}]], ControlType -> SetterBar},
 {{a0, 1, a}, 1, 4}, {{b0, 0, b}, 0, 10}
 ]

Mathematica graphics

Update 2

I had already put the dynamic updating in the selection bar so that they would reflect the current parameters a and b. I didn't realize you were going to add a plot label. The code below does both. To get rid of the parameters in the SetterBar, change

Pane[TraditionalForm@NumberForm[# /. {a -> a0, b -> b0}, 3], 78, Alignment -> Center]

to just TraditionalForm[#] or StandardForm[#] or whatever formatting you wish.

types = {"Algebraicas", "Logaritmicas y exponenciales", 
   "Trigonometricas", "Trigonometricas Inversas"(*,"Hiperbolicas",
   "Hiperbólicas Inversas"*)};
functions = {
   {Sqrt[a x + b], a x^2 + b, a (x - b)^3, a Abs[x - b]},
   {Log[10, 1000], Log[E, x], Log[1000.]},
   {Sin[a x + b], Cos[a x + b], Tan[a x + b]},
   {Cot[a x + b], Csc[a x + b], Sec[a x + b]}};

Manipulate[
 selection = type /. Thread[types -> functions[[All, 1]]];
 Dynamic@Plot[selection /. {a -> a0, b -> b0}, {x, -5, 5}, 
   PlotRange -> {{-5, 5}, {-10, 10}}, PlotStyle -> {Blue, Thick}, 
   PlotLabel -> Pane[NumberForm[selection /. {a -> a0, b -> b0}, 3], {Automatic, 20}]],

 {type, types, ControlType -> PopupMenu}, {selection, 
  Dynamic[type /. 
    Thread[types -> With[{selections = 
              Map[# -> Pane[TraditionalForm @ NumberForm[# /. {a -> a0, b -> b0}, 3],
                            78, 
                            Alignment -> Center] &,
                  functions, {2}]},
           selections]]],
   ControlType -> SetterBar},
 {{a0, 2.}, 1., 4.}, {{b0, 3.}, 0., 10.}
 ]

Manipulate output

Ok, it reduces the code much more but I need to do is you can move the graph parameters — Starlight, Oct 06 '13 at 18:27
Thanks was just what I wanted understood the code you used as it is too strange for me. — Starlight, Oct 11 '13 at 16:21
Hello again, I have a problem I'm manipulating your code but I want to display the label of the function but does not update when you move the slider, as I can do to update? — Starlight, Oct 11 '13 at 16:46
I don't understand. Which label? Do you mean you want the a and b in the SetterBar selection to be dynamically update when the a0/b0 sliders are moved? — Michael E2, Oct 11 '13 at 19:29
Exactly want to be updated on the top will put the code that I have to observe what happens. — Starlight, Oct 12 '13 at 19:29
Did you try the change I mentioned above, Pane[TraditionalForm[..]] to just TraditionalForm[#]? Your posted code does not have it. — Michael E2, Oct 14 '13 at 21:01
Even so it does not work keep changing SetterBar values, put the new code in the top — Starlight, Oct 15 '13 at 16:11
You still have Pane[TraditionalForm@NumberForm[# /. {a -> a0, b -> b0}, 3], 78, Alignment -> Center] in your code. — Michael E2, Oct 15 '13 at 16:53
Now when I compile I initialized with the first Plot graphs of each type, as it off?,I add the code :) — Starlight, Oct 17 '13 at 21:13

How I can make a menu with different graphs with modifiable parameters?

1 Answers1

Linked