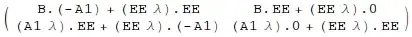Keep order of mulciplication in Matrix production

Question

{{λ E, B}, {λ A1, λ E}}.{{E, 0}, {-A1, E}}

\begin{align*}\left(\begin{array}{cc} E^2 \lambda -A1 B & B E \\ 0 & E^2 \lambda \\\end{array}\right)\end{align*}

The result is not quit true, since $A1 B$ may not equal to $B A1$ when $A1$ and $B$ are block matrix.

Just some observations: 1. E is a special symbol in Mathematica (base of natural logarithm) 2. "0" presumaly is a block matrix but as written Mathematica will interpret as a number 3. Symbolically given 0 and E the commutative assumption follows. This would not be the case if you entered matrices (of appropriate dimensions). — ubpdqn, Oct 06 '13 at 12:16

score 2 · Answer 1 · answered Oct 06 '13 at 12:18

One option is to define your own matrix-multiplication function, such as:

ClearAll[mmult];
mmult[a_?MatrixQ, b_?MatrixQ, multF_: Times] :=
   Outer[Inner[multF, ##, Plus] &, a, Transpose @ b, 1, 1]

With the default multiplication function, it would return the same result (although probably much less efficiently):

mmult[{{\[Lambda] E,B},{\[Lambda] A1,\[Lambda] E}},{{E,0},{-A1,E}}]

(* {{-A1 B+E^2 \[Lambda],B E},{0,E^2 \[Lambda]}}  *)

But you can also supply your own function:

mmult[{{\[Lambda] E, B}, {\[Lambda] A1, \[Lambda] E}}, {{E, 0}, {-A1, E}}, mult]

(* 
   {
     {mult[B, -A1] + mult[E \[Lambda], E], mult[B, E] + mult[E \[Lambda], 0]},
     {mult[A1 \[Lambda], E] + mult[E \[Lambda], -A1], mult[A1 \[Lambda], 0] + mult[E \[Lambda], E]}
   }
*)

score 2 · Answer 2 · edited Apr 13 '17 at 12:55

You can use Inner as a generalization of Dot

Inner[Dot, {{λ EE, B}, {λ A1, λ EE}}, {{EE, 0}, {-A1, EE}}, Plus] // MatrixForm

enter image description here

I use EE instead of E because E is reserved as the exponential constant $e$.

Then it can be simplified (in Mathematica 9)

$Assumptions = λ \[Element] Complexes;
TensorExpand[%%] /. {M_ .EE :> M, EE.M_ :> M} // MatrixForm

There is a problem with simplification of identity matrices (see here) so I use exact pattern replacements.

enter image description here

Keep order of mulciplication in Matrix production

2 Answers2

Linked