22

Given a directed acyclic graph, I want to remove all the edges $v_i \rightarrow v_j$ if $v_j$ is reachable from $v_i$ by some other path. Given the rich set of graph algorithms in Mathematica, what is the best way to achive this?

The background of the problem is this. I have a list of jobs and their dependencies, e.g., $a \rightarrow b$ means job $b$ can start only when job $a$ finishes. A list $\{a \rightarrow b, b \rightarrow c, a \rightarrow c\}$ is redundant because $a \rightarrow c$ is implied. I want to reduce the dependencies to a bare minimum.

m_goldberg
  • 107,779
  • 16
  • 103
  • 257
asterix314
  • 1,325
  • 8
  • 19
  • Algorithms I've looked at: minimum spanning tree, edge/vertex cover, shortest paths. But they are not what I'm looking for. – asterix314 Oct 08 '13 at 06:21
  • 1
    Including working code and showing what you already tried and what your input/output should look like will improve your chances to get an answer and make this question more useful for future visitors. At the moment there is about no Mathematica reference, too. – Yves Klett Oct 08 '13 at 06:34
  • 1
    The solutions people have contributed are all of the "roll your own" type. It's a pity the rich set of graph algorithms in Mathematica are left unutilized for this question while we start from scratch. – asterix314 Oct 10 '13 at 15:42
  • 1
    The action that does this is called Transitive Reduction, explained in detail at https://en.wikipedia.org/wiki/Transitive_reduction – Evgeny Zislis Dec 10 '19 at 08:54

4 Answers4

11

Let $A$ be the adjacency matrix of the graph to be reduced. $A$ is also the reachability matrix for 1 hop, and $A^2$ for 2 hops and so on, if we substitue logical and ($\land$) for multiplication and logical or ($\lor$) for addition in multiplying two matrices. $A^k$ ($k<n$) will eventually be all zeros because we cannot have a path of $n$ hops or more where $n$ is the number of vertices (assuming no cycles).

Let $S = A^2 \lor A^3 \lor \cdots \lor A^k$ be the reachability matrix of 2 or more hops. To reduce $A$, we need to remove $i \rightarrow j$ in $A$ if it is also in $S$. The reduced adjacency matrix is therefore $A \land \lnot S$.

To put the above into code, note that we can just use normal multiplication and addition, after all, if we only look at the sign. This has a huge performance boost because we will be using highly optimized matrix multiplications on machine integers. We'll use Unitize to keep the intermediate results within the range of machine intergers:

reduce[a_] := a (1 - FixedPoint[Unitize[a.(a + #)] &, a.a])
asterix314
  • 1,325
  • 8
  • 19
  • Neatly compacted! This seems to be 2x faster than my code working directly on Graphs, you should consider accepting your own answer :) – István Zachar Oct 11 '13 at 14:02
7

I do not have experience with graphs and built-in functions related to them, but maybe something based on fact that the following is a Tautology:

$(a\Rightarrow b)\land (b\Rightarrow c)\Rightarrow (a\Rightarrow c)$

 And[Implies[a, b], Implies[b, c]]~Implies~Implies[a, c] // Simplify

True

Edit I've added temporary replacement for 1 and 0 which can cause a problems since they are interpreted by Simplify as True and False. More there: Simplify assumes..

list = {DirectedEdge[a, b], DirectedEdge[b, c], DirectedEdge[a, c]}; 

reduce[list_] := Module[{a, b}, With[{impl = Implies @@@ list /. {1 -> a, 0 -> b}},
     DirectedEdge @@@ MapIndexed[
                         If[TrueQ @ Simplify @ Implies[And @@ Drop[impl, #2], #1], 
                            Unevaluated[Sequence[]], #1] &
                         , impl]
                       ] /. {a -> 1, b -> 0}]

reduce[list]

{DirectedEdge[a, b], DirectedEdge[b, c]}

Edit by m_goldberg

I think it is is worth looking at some graphs a little more complex than the one the OP mentioned, both before and after reduce is applied to them.

dag2 = DirectedEdge @@@ {{a, b}, {b, c}, {a, c}, {e, b}, {e, c}};
dag3 = DirectedEdge @@@ {{a, b}, {b, c}, {a, c}, {e, b}, {e, c}, {e, f}, {f, c}};
dag4 = DirectedEdge @@@ {{2, 1}, {3, 1}, {3, 2}, {4, 1}, {4, 2}, {4, 3}, {5, 1}, 
                         {5, 2}, {5, 3}, {5, 4}}; (*István's example*)


dags = {#, reduce[#]} & /@ {dag2, dag3, dag4}
gridData = Prepend[
             Map[Graph[#, VertexLabels -> "Name", GraphLayout -> "SpringEmbedding"] &,
                 dags, {2}], 
             {"Before", "After"}];
Grid[gridData, Frame -> All]

enter image description here

Community
  • 1
Kuba
  • 136,707
  • 13
  • 279
  • 740
  • I think it does work well. I had to do some testing with a couple of more interesting data sets to convince myself of it. Since I had the test notebook at hand, I thought why not post the tests as an illustration of the method? – m_goldberg Oct 08 '13 at 09:01
  • @m_goldberg good idea, feel free to edit it whenever you want. – Kuba Oct 08 '13 at 09:08
  • 1
    Thanks Kuba for the clever idea of reformulating the problem using the language of logic. Along the same lines I got the following: reduce2[list_] := With[{impl = And @@ (list /. DirectedEdge -> Implies)}, List @@ BooleanMinimize[impl, "CNF"] /. {! a_ || b_ :> DirectedEdge[a, b], b_ || ! a_ :> DirectedEdge[a, b]}] – asterix314 Oct 08 '13 at 09:13
  • I was actually looking for graph-specific algorithms. This detour to the logic method is very refreshing indeed. But there must be a graph algorithm to it, too? – asterix314 Oct 08 '13 at 09:21
  • 1
    @asterix314 I'm glad you find it useful. To make it even more compact you can write Implies @@@ list instead of list /. DirectedEdge->Implies. I used this because I'm not experienced with Graphs. So maybe better hold on with an accept to not discourage others in finding quicker way :) – Kuba Oct 08 '13 at 09:23
6

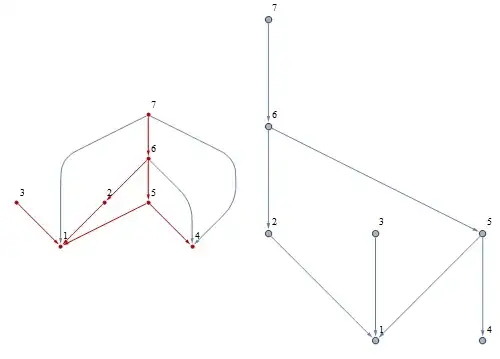
I used this generator algorithm for DAGs (by Szabolcs):

{vertices, edges} = {7, 10};
elems = RandomSample@PadRight[ConstantArray[1, edges], vertices (vertices-1)/2];
adj = Take[FoldList[RotateLeft, elems, Range[0, vertices-2]], All, 
           vertices]~LowerTriangularize~-1;
g = AdjacencyGraph[adj, DirectedEdges -> True];
EdgeList@g

{2 -> 1, 3 -> 1, 3 -> 2, 4 -> 1, 4 -> 2, 4 -> 3, 5 -> 1, 5 -> 2, 5 -> 3, 5 -> 4}

Removing redundant edges iteratively:

new = Graph[Flatten[If[GraphDistance[EdgeDelete[g, #], First@#, 
            Last@#] < Infinity, {}, #] & /@ EdgeList@g], 
         VertexLabels -> "Name", ImagePadding -> 10];
Row@{HighlightGraph[g, new, VertexLabels -> "Name", ImagePadding -> 10], new}

Mathematica graphics

For some graphs, the remaining graph is simply the path graph of the topologically sorted vertices:

g = Graph[{2->1, 3->1, 3->2, 4->1, 4->2, 4->3, 5->1, 5->2, 5->3, 5->4}];

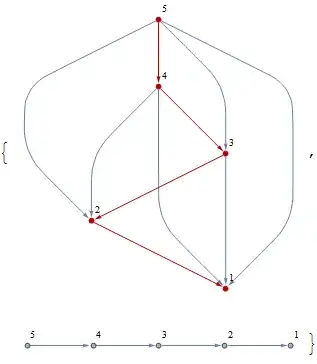
Mathematica graphics

Note that this method removes unconnected singletons.

Adjacency matrix version

Here is a version that works directly on adjacency matrices. This should be faster than working on huge Graph objects directly.

The removableQ function recursively tests if the node from has an alternative route to to than the direct one, by collecting children nodes. The moment the function finds another edge terminating at to, exits from the loop, as it is unnecessary to check further.

removableQ[m_, {from_, to_}] := Module[{children},
   children = Flatten@Position[m[[from]], 1];
   If[MemberQ[children, to], Throw@to, 
    Do[removableQ[m, {i, to}], {i, children}]; None]
   ];

The wrapper reduce iterates through all edges in the matrix:

reduce[adj_] := Module[{edgeList = Position[adj, 1], rem},
   rem = DeleteCases[{First@#, 
        Catch@removableQ[ReplacePart[adj, # -> 0], #]} & /@ 
      edgeList, {_, None}];
   ReplacePart[adj, Thread[rem -> 0]]
   ];

Let's call reduce on a random DAG's adjecency matrix:

g = DirectedGraph[RandomGraph[{6, 10}], "Acyclic"];
EdgeList@g

{1 -> 3, 1 -> 4, 1 -> 5, 1 -> 6, 2 -> 3, 2 -> 4, 2 -> 5, 3 -> 5, 4 -> 6, 5 -> 6}

adj = Normal@AdjacencyMatrix@g
new = reduce@adj;
Row@{g, AdjacencyGraph@new}

Mathematica graphics

Note that this method does not remove unconnected singletons.

Community
  • 1
István Zachar
  • 47,032
  • 20
  • 143
  • 291
  • Strange, my reduce drops 1 and leaves 5->4->3->2 for the last case of yours. – Kuba Oct 08 '13 at 09:55
  • @Kuba It should keep 1. I still cannot figure out whether there is always one exact reduction or it could depend on the order edges are removed. – István Zachar Oct 08 '13 at 10:02
  • @Kuba It removes the 1 because Simplify@Implies[(3 => 1) && (3 => 2), 2 => 1] returns True, though it shouldn't for a graph (if you have edges 3->1 and 3->2 you don't necessarily have 2->1)! – István Zachar Oct 08 '13 at 10:12
  • Or rather pay attention to 1 an 0 which are interpreted by logical functions ;) Implies["a", 1] // Simplify – Kuba Oct 08 '13 at 10:23
  • 1
    @Kuba Oh, sure, that buglike feature got me once. Quite annoying! – István Zachar Oct 08 '13 at 10:32
  • I'm going to accept this for now as it wins in terms of performance. The run time of @Kubma's Simplfy-based algorithm is quite intractable when the number of edges gets large, say 100. – asterix314 Oct 08 '13 at 12:28
  • @asterix314 Yes, Simplify could be a huge bottleneck. If you really have to work on huge graphs, I'll try to come up with a more direct approach that only uses adjacency matrices. That could be a few magnitudes faster than working on Graph objects. Thanks for the accept. – István Zachar Oct 08 '13 at 14:05
  • Here is a more concise formulation based on @IstvánZachar's method: Let A be the adjacency matrix of the original graph. A represents also the single hop reachablility, and A^k for k hops, etc. Here we use And for Times and Or for Plus. The reachability matrix of more than 1 hop is thus S = A^2 + A^3 + ... + A^(n-1). The reduced adjacency matrix is thus And[A, !S]. Or in code:

    reduce2[x_] := Block[{CenterDot = Function[{a, b}, Inner[BitAnd, a, b, BitOr]]}, BitAnd[x, 1 - BitOr @@ Drop[FixedPointList[CenterDot[#, x] &, CenterDot[x, x], -2]]]]

     – asterix314 Oct 10 '13 at 06:11
  • @asterix314 Nice solution, I think you should make that an individual answer! Just to note, the last argument (-2) for FixedPointList doesn't seem to work on my machine, drops error messages. Without it the code is fine. – István Zachar Oct 10 '13 at 06:53
  • @IstvánZachar Sorry the -2 is for Drop[] actually, because the last 2 elements in the FixedPointList[] are all 0s. Without the Drop the code should also work though. It is worth mentioning that the run time of this concise solution is not so good as yours. – asterix314 Oct 10 '13 at 07:42
  • @asterix314 Still I suggest to put it up as an answer as it is really concise and reflects the nice synergies of matrix operations on graphs. – István Zachar Oct 10 '13 at 07:57
  • OK I'll put it up later after I learn some formating basics ... – asterix314 Oct 10 '13 at 08:19
  • @asterix314 you don't need to define your dot with Inner. You could do the following and it makes code much faster with sparse array: reduce3[x_] := BitAnd[x, 1 - BitOr @@ Drop[FixedPointList[Unitize[Dot[#1, x]] &, Unitize[Dot[x, x]]], -2]] – halmir Oct 10 '13 at 14:42
  • @halmir yes exactly. See my answer. I got rid of all logical operations (I didn't know Unitize so i used Sign instead). – asterix314 Oct 10 '13 at 15:23
3

TransitiveReductionGraph (version 10+)

Using the examples from @Kuba's answer:

dag1 = {DirectedEdge[a, b], DirectedEdge[b, c], DirectedEdge[a, c]};
dag2 = DirectedEdge @@@ {{a, b}, {b, c}, {a, c}, {e, b}, {e, c}};
dag3 = DirectedEdge @@@ {{a, b}, {b, c}, {a, c}, {e, b}, {e, c}, {e,  f}, {f, c}};
dag4 = DirectedEdge @@@ {{2, 1}, {3, 1}, {3, 2}, {4, 1}, {4, 2}, {4, 3},
  {5, 1}, {5, 2}, {5, 3}, {5, 4}};
options = {VertexLabels -> Placed["Name", Center], VertexSize -> Large, ImageSize -> Small}
    
Grid[Prepend[Through[{Graph[#, options]&, TransitiveReductionGraph[#, options]&}@#] & /@ 
  {dag1, dag2, dag3, dag4},
 {Style["g", 16, Bold], Style["TransitiveReductionGraph[g]", 16, Bold] }],
 Dividers -> All, ItemSize -> {{Scaled[.3], Scaled[.3]}, {Scaled[.1], 5, 5, 5, 5}}]

enter image description here

Note: Although it works as expected in the cases considered here, as noted by Szabolcs, TransitiveReductionGraph had unresolved issues before version 12.1.

kglr
  • 394,356
  • 18
  • 477
  • 896