How can I create an image like this

Question

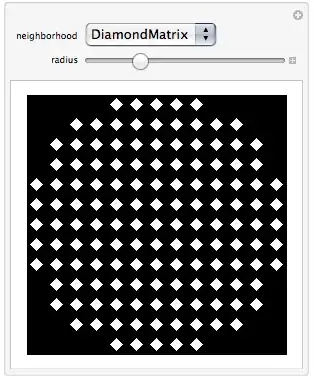
I'm trying to get an algorithm that generates a picture like this

enter image description here

So far I've tried a little something with the help of the knowledge center, getting a graphics grid of squares already. But what now? I'm completely in the dark on how to trim it in the circle-shape I want. (If there are better solutions out there, please forget what I have started with. My only goal is to get the end result where I can make a pattern like this with variable size in terms of diameter in squares, size of the squares themselves and spacing in between.)

size = 10;
scalesize = 1;
table1 = Table[Graphics[Rectangle[]], {size}, {size}];

GraphicsGrid[table1, Frame -> None, Spacings -> Scaled[scalesize]]

score 22 · Accepted Answer · answered Oct 18 '13 at 04:20

22

The only thing you need for the underlying data is DiskMatrix. The rest of the visualization can be chosen freely:

ArrayPlot[ArrayPad[DiskMatrix[7], 1], ColorFunction -> GrayLevel, 
 Mesh -> All, MeshStyle -> Directive[Thickness[.02], Black]]

Mathematica graphics

answered Oct 18 '13 at 04:20

halirutan

112,764
7
263
474

3

I like those dots in knots of the mesh :) – Kuba Oct 18 '13 at 06:16
Thank you so much, I tried spitting through the database for two days getting to find such a function. – Sward Oct 18 '13 at 19:03

s0rce · Answer 2 · 2013-10-20T20:38:48.640

Here is an example using graphics primitives. It has some nice flexibility.

radius = 6.5;
sidelength = 0.6;
xy = Flatten[
   Table[{x, y}, {x, -2 radius, 2 radius}, {y, -2 radius, 2 radius}], 
   1];
inside = Select[xy, EuclideanDistance[#, {0, 0}] <= radius &];
shape[center_, a_] := {White, Rectangle[center - a/2, center + a/2]}
Graphics[shape[#, sidelength] & /@ inside, Background -> Black]

Based on other answers it is simpler and more elegant to replace Table, Select and EuclideanDistance with DiskMatrix making a nice little one-liner

Graphics[{White, Rectangle[# - 0.3, # + 0.3]} & /@ Position[DiskMatrix[6], 1], Background -> Black]

Mathematica graphics

Let's redefine the shape function:

shape[center_,a_] := {White, Disk[center, a/2]}
Graphics[shape[#, sidelength] & /@ inside, Background -> Black]

Mathematica graphics

and again:

starcoords := 
  With[{r = RandomReal[Pi]}, 
   Table[{Cos[t + r], Sin[t + r]}, {t, 0, 4 Pi, 4 Pi/5}]/3];
shape[center_] := {White, Polygon[center + # & /@ starcoords]}
Graphics[shape /@ inside, Background -> Black]

Mathematica graphics

This does the job too perfectly, without the use of DiskMatrix, which was frankly unfindable by me. I don't think I could have ever found out how to do this. I'd like to select your answer as accepted answer too, but I can only select one unfortunately. — Sward, Oct 18 '13 at 19:04

bill s · Answer 3 · 2013-10-20T22:32:26.883

5

Here is an answer using image processing techniques rather than graphics, that is also very flexible. Create an array of dots at the centers of all the shapes:

dots = Image[Upsample[DiskMatrix[8], 20, 10]];

enter image description here

and then convolve with the desired shape. The shape is then replicated throughout the image. For the requested box:

ImageConvolve[dots, BoxMatrix[5]]

enter image description here

Any shape will do: here is how to stick a cross at each dot.

ImageConvolve[dots, CrossMatrix[5]]

enter image description here

Borrowing cormullion's idea of making it interactive:

Manipulate[dots = Image[Upsample[DiskMatrix[6], 20, 10]]; 
  ImageConvolve[dots, neighborhood[radius]],
  {neighborhood, {IdentityMatrix, DiskMatrix, BoxMatrix, CrossMatrix, 
      DiamondMatrix, GaussianMatrix}}, {radius, 1, 21, 1}]

enter image description here

edited Oct 20 '13 at 22:32

answered Oct 20 '13 at 14:28

bill s

68,936
4
101
191

If you add an ArrayPad you can center your shapes. dots = Image[Upsample[ArrayPad[DiskMatrix[8], {1, 0}], 20]]; – s0rce Oct 20 '13 at 14:39
You can also use the 2nd argument of Upsample but then the border is quite narrow. – s0rce Oct 20 '13 at 14:53
@sOrce -- Thanks... I've updated so as to center the dots and shapes. – bill s Oct 20 '13 at 15:04

score 4 · Answer 4 · answered Oct 18 '13 at 09:55

4

I tried to make a Manipulate, but there are some errors in this code due possibly to rounding errors which I haven't tracked down:

Manipulate[
 Graphics[{
    White,
    Table[
     Rectangle[{x, y}, {x + space, y + space} ], {y, 1, n, step}, {x, 
      1, n, step}]
    }, Background -> Black] /. 
  Rectangle[{x_, y_}, {x1_, 
      y1_}] /; (n/2 - Norm[x, x + step + space])^2 + (n/2 - 
         Norm[y, y + step + space])^2 > radius :> {Black, 
    Rectangle[{x, y}, {x1, y1}]},
 {n, 10, 100, 2},
 {space, 1, step},
 {step, 5, 10, 1},
 {radius, 1, 1000}
 ]

a manipulate for designing grids

answered Oct 18 '13 at 09:55

cormullion

24,243
4
64
133

I do appreciate your effort a lot :), but the above two anwers don't have these rounding errors. – Sward Oct 18 '13 at 19:05
@sward no problem - I didn't spend too much time on it, but I thought the method might be interesting to try. Unfortunately allowing everything to be a variable brings new problems... :) – cormullion Oct 18 '13 at 19:08

How can I create an image like this

4 Answers4