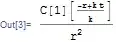PDE Solving in mathematica

Question

I'd like to ask how I might go about solving this equation:

$\frac{\partial Ci}{\partial t} + \frac{1}{r^2}\frac{\partial (r^2 Ci)}{\partial r} = D\frac{1}{r^2}\frac{\partial}{\partial r}(r^2\frac{\partial Ci}{\partial r})$

as suggested a simplification

$\frac{\partial Ci}{\partial t} + \frac{1}{r}2Ci +\frac{1}{r^2}\frac{\partial Ci}{\partial r} = D(\frac{2}{r}\frac{\partial Ci}{\partial r} +\frac{\partial^2 Ci}{\partial r^2})$

$r = 0, t = 0 \rightarrow Ci = 0$
$r = 1, t = 0 \rightarrow Ci = 0$

I am fairly new to Mathematica and I don't really know how to go about this; I've also tried the steps outlined in this post here but while I understood what to do I get recursion limit reached errors (using the code provided).

Could you please help me out on how to solve this equation?

a partial and first attempt on solving this taking in account the notes of the posted link is the following:

Clear[y];
f1[r_ /; r > 0] := 1;
f1[r_ /; r == 0] := 2;
f2[r_ /; r > 0] := 1/r^2;
f2[r_ /; r == 0] := 0;
f3[r_ /; r > 0] := 1/r;
f3[r_ /; r == 0] := 0;
eqns = {

  Derivative[0, 0, 1][y][t, r, z] +

  f3[r]2y[t, r, z] +
  f2Derivative[0, 1, 0][y][t, r, z] -
  2f3[r]Derivative[0, 1, 0][y][t, r, z] -
  Derivative[0, 2, 0][y][t, r, z] == Derivative[1, 0, 0][y][t, r, z],
  y[t, 0, z] == 0,
  y[t, r, 0] == 0,
  Derivative[0, 1, 0][y][t, 0, z] == 0,
  Derivative[0, 0, 1][y][t, r, 0] == 0,
  y[0, r, z] == (1 - r^2)(1 - z^2)}
$RecursionLimit = 1536
y[t_, r_, z_] = 
     y[t, r, z] /. 
          First[NDSolve[eqns, y[t, r, z], {t, 0, 1}, {r, 0, 1}, {z, 0, 1}, 
          Method -> {"MethodOfLines", Method -> "StiffnessSwitching", 
          "DifferentiateBoundaryConditions" -> {True, 
          "ScaleFactor" -> 1}}]];

This gives me a lot of errors but the first one is the following:

Answer 1

Here is a solution using the method of characteristics. But the conditions as given above will cause a problem at $r=0$. There is no Cauchy data to use. So I kept the solution in terms of the constants of integrations.

Let $u\left( t,r\right) $ be the solution

\begin{align*} \frac{\partial u}{\partial t}+\frac{1}{r^{2}}\frac{\partial\left( r^{2}u\right) }{\partial r} & =D\frac{1}{r^{2}}\frac{\partial\left( r^{2}u\right) }{\partial r}\\ \frac{\partial u}{\partial t}+\frac{1}{r^{2}}\left( 2ru+r^{2}\frac{\partial u}{\partial r}\right) & =D\frac{1}{r^{2}}\left( 2ru+r^{2}\frac{\partial u}{\partial r}\right) \\ \frac{\partial u}{\partial t}+\left( 2\frac{u}{r}+\frac{\partial u}{\partial r}\right) & =D\left( 2\frac{u}{r}+\frac{\partial u}{\partial r}\right) \\ \frac{\partial u}{\partial t}+\frac{\partial u}{\partial r}\left( 1-D\right) & =-2\frac{u}{r}\left( 1-D\right) \end{align*}

Let $1-D=k$, hence

\begin{align*} \frac{\partial u}{\partial t}+k\frac{\partial u}{\partial r} & =-2k\frac {u}{r}\\ \frac{1}{k}\frac{\partial u}{\partial t}+\frac{\partial u}{\partial r} & =-2\frac{u}{r} \end{align*}

To find the solution using the characteristics method, we write the above in the standard form

$$ \frac{dt}{k^{-1}}=\frac{dr}{1}=\frac{du}{-2\frac{u}{r}}% $$

Hence $dt=\frac{dr}{k}$ or $t=\frac{r}{k}+r_{0}$ or $$ r_{0}=t-\frac{r}{k} $$ Also, $\frac{du}{-2\frac{u}{r}}=dt$ or $\frac{du}{u}=-\frac{2}{r}dt$, hence $\ln u=-\frac{2}{r}t+c_{2}$, or $u=Ae^{-\frac{2t}{r}}$.

At $t=0$, to satisfy initial conditions at $r_{0}$, then $u\left( 0,r_{0}\right) =f\left( r_{0}\right) =A$. So the solution is $$ u\left( t,r\right) =A\left( t-\frac{r}{k}\right) e^{-\frac{2kt}{r}}% $$

Mathematica gives this btw:

  ClearAll[u, r, t, k];
  ode = D[u[r, t], t] + k D[u[r, t], r] + 2 k u[r, t]/r
  sol = u[r, t] /. First@DSolve[ode == 0, u[r, t], {r, t}]

Again, I think the initial conditions given are not correct.

see http://reference.wolfram.com/mathematica/howto/SolveAPartialDifferentialEquation.html

for more information.