There is a problem with the initial conditions. At $x=0$ there is no solution. The analytical solution given by Mathematica seems to have used the standard solution for standard Bessel ODE http://mathworld.wolfram.com/BesselDifferentialEquation.html, which is a Bessel function. But I am not sure for $n=0$ one can just use Bessel(0,x), I think BesselY(0,x) is also needed.
This is what I get.
But to answer you, I think you need to use series solution for this. Or avoid $x=0$ as was suggested in the comment for a numerical solution.
\begin{align*}
y^{\prime\prime}\left( x\right) +\frac{1}{x}y^{\prime}\left( x\right)
+y\left( x\right) & =0\\
y\left( 0\right) & =1\\
y^{\prime}\left( 0\right) & =0
\end{align*}
Let $x=e^{z}$ or $\ln\left( x\right) =z$, hence $\frac{dy}{dx}=\frac{dy}
{dz}\frac{dz}{dx}=\frac{dy}{dz}\frac{1}{x}$ and $\frac{d^{2}y}{dx^{2}}
=\frac{d^{2}y}{dz^{2}}\frac{dz}{dx}\frac{1}{x}+\frac{dy}{dz}\left( \frac
{-1}{x^{2}}\right) =\frac{d^{2}y}{dz^{2}}\frac{1}{x^{2}}-\frac{1}{x^{2}}
\frac{dy}{dz}$
Substituting all these back into the original ODE gives
\begin{align*}
\frac{d^{2}y}{dz^{2}}\frac{1}{x^{2}}-\frac{1}{x^{2}}\frac{dy}{dz}+\frac{1}
{x}\frac{dy}{dz}\frac{1}{x}+y\left( z\right) & =0\\
\frac{d^{2}y}{dz^{2}}+x^{2}y\left( z\right) & =0\\
\frac{d^{2}y}{dz^{2}}+e^{2z}y\left( z\right) & =0
\end{align*}
The solution to the above is
$$
y\left( z\right) = BesselJ_{0}\left( \sqrt{e^{2z}}\right)
c_{1}+2 BesselY_{0}\left( \sqrt{e^{2z}}\right) c_{2}
$$
Replacing back
\begin{equation}
y\left( x\right) = BesselJ_{0}\left( x\right) c_{1}
+2 BesselY_{0}\left( x\right) c_{2}\tag{1}
\end{equation}
You see that there is a BesselY[0,x] function in the solution which do not show up the solution given by Mathematica for some reason.
Now to find the constants $c_{1},c_{2}$ we use initial conditions. At $x=0,y=1\,\ $,hence
$$
1=c_{1}-\infty
$$
For the derivative at $x=0$,
$$
y^{\prime}\left( x\right) =- BesselJ_{1}\left( x\right)
c_{1}-2 BesselY_{1}\left( x\right) c_{2}
$$
At $x=0$
$$
0=0-\infty
$$
sol = DSolve[{y''[z] + Exp[2 z] y[z] == 0}, y[z], z]
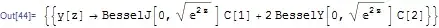
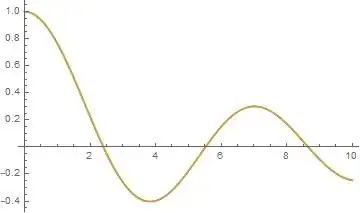
Btw, Maple 17 gives a numerical solution for this, without the 1/0 issue. But I am not sure how it avoided the point $x=0$ now. It uses RK45 standard numerical method. Here it is:

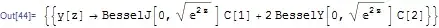


DSolve, though I also get the answer you show. – bill s Oct 20 '13 at 17:090making trouble with a small number :sol[x_] = First[y[x] /. NDSolve[{y''[x] + 1/x y'[x] + y[x] == 0, y[$MachineEpsilon] == 1, y'[$MachineEpsilon] == 0}, y[x], {x, $MachineEpsilon, 10}]]. – b.gates.you.know.what Oct 20 '13 at 17:18