How to increase Spectrogram resolution?

Question

I have a time-domain signal that I want do a time-frequency analysis on it. When I tried the Spectrogram, I always get very low resolution.

For example:

I have a signal like this:

data = Table[
   Piecewise[{{Sin[2 \[Pi] 10 t], 0 <= t < 1/4}, {Sin[2 \[Pi] 25 t], 
      1/4 <= t < 1/2}, {Sin[2 \[Pi] 50 t], 
      1/2 <= t < 3/4}, {Sin[2 \[Pi] 100 t], 3/4 <= t <= 1}}], {t, 0, 
    1, 1/1023}];
ListLinePlot[data, AspectRatio -> 0.2]

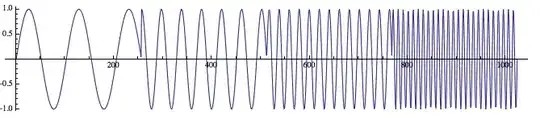
enter image description here

when I do a wavelet transform, I get a result that I can identify each frequency and their arrival time.

cwd = ContinuousWaveletTransform[data, GaborWavelet[6], {Automatic, 12}];
freq = (1023/(#*GaborWavelet[6]["FourierFactor"])) & /@ (Thread[{Range[8], 1}] /. cwd["Scales"]);
ticks = Transpose[{Range[Length[freq]], freq}];
WaveletScalogram[cwd, Frame -> True, FrameTicks -> {{ticks, Automatic}, Automatic},FrameLabel -> {"Time", "Frequency(Hz)"}, ColorFunction -> "RustTones"]

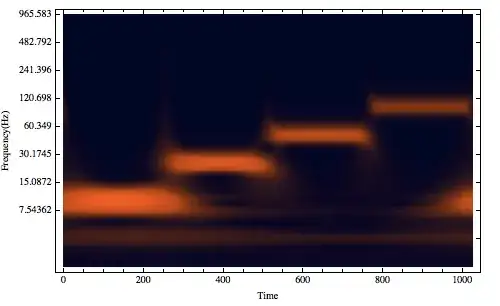
enter image description here

The wavelet transform is very good for me except I prefer a linear scale instead of a log scale. So I tried the Spectrogram.

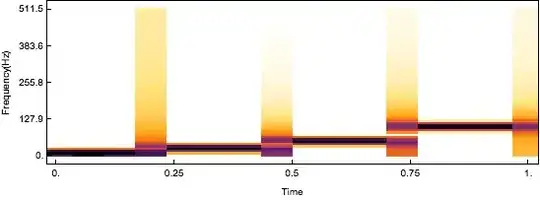
Spectrogram[data, SampleRate -> 1023, ColorFunction -> "RustTones", FrameLabel -> {"Time", "Frequency(Hz)"}]

enter image description here

From the spectrogram I can barely see that there are four frequencies components, but the resolution is very low compared to the wavelet transform, and there seems be a lot of "noise" in it. So how can I use Spectrogram to plot a similar result as that of wavelet transform, a result that I can easily see the difference frequencies and their occurrence in time?

Edit:

Second example

data2 = {0.0000688553, 0.0000688557, 0.0000688564, 0.000068857, 0.0000688571, 0.0000688563, 0.0000688551, 0.000068854, 0.0000688539,0.0000688551, 0.0000688573, 0.0000688591, 0.0000688593, 0.0000688572, 0.0000688536, 0.0000688507, 0.0000688504, 0.0000688538, 0.0000688594, 0.0000688641, 0.0000688644, 0.0000688591, 0.0000688504, 0.0000688431, 0.0000688426, 0.0000688506, 0.0000688639, 0.0000688747, 0.0000688756, 0.0000688636, 0.0000688439, 0.0000688279, 0.0000688268, 0.0000688443, 0.0000688727, 0.0000688957, 0.0000688975, 0.0000688724, 0.0000688318, 0.0000687991, 0.0000687969, 0.0000688321, 0.0000688886, 0.0000689341, 0.0000689375, 0.000068889,0.0000688108, 0.0000687484, 0.0000687447, 0.0000688111, 0.0000689165, 0.0000690002, 0.0000690059, 0.0000689171, 0.0000687754, 0.000068664, 0.0000686589, 0.000068778, 0.0000689632, 0.000069108, 0.0000691159, 0.0000689611, 0.0000687182, 0.0000685311,0.0000685273, 0.0000687314, 0.0000690404, 0.0000692758, 0.0000692824, 0.0000690239, 0.0000686276, 0.000068331, 0.0000683373,0.0000686747, 0.0000691661, 0.0000695268, 0.0000695212, 0.0000691047, 0.0000684868, 0.0000680431, 0.0000680816, 0.0000686216, 0.0000693686, 0.0000698882, 0.0000698443, 0.0000691941, 0.0000682709, 0.0000676461, 0.0000677627, 0.0000686028, 0.0000696891, 0.0000703884, 0.000070254, 0.0000692688,0.0000679463, 0.0000671236, 0.0000674037, 0.0000686737, 0.0000701814, 0.0000710486, 0.0000707318, 0.0000692847, 0.0000674719, 0.0000664738, 0.0000670596, 0.0000689181, 0.0000709029, 0.0000718656, 0.0000712238, 0.0000691734, 0.0000668091, 0.0000657258, 0.000066827, 0.000069441, 0.0000718908, 0.0000727864, 0.0000716293, 0.0000688506, 0.0000659424, 0.0000649574, 0.0000668415, 0.0000703392, 0.0000731224, 0.0000736827, 0.0000718041, 0.0000682428, 0.0000649098, 0.0000643029, 0.000067249, 0.0000716496, 0.0000744731, 0.0000743462,0.0000715934, 0.0000673322, 0.0000638262, 0.0000639329, 0.0000681481, 0.0000732907, 0.0000757007, 0.0000745275, 0.0000708955, 0.0000662018, 0.0000628777, 0.0000639981, 0.0000695195, 0.000075033, 0.0000764844, 0.0000740176, 0.0000697294,0.0000650442, 0.0000622699, 0.0000645526, 0.0000711839, 0.0000765324, 0.0000765193, 0.0000727403, 0.0000682638, 0.0000641159, 0.0000621449, 0.000065499, 0.000072824, 0.0000774271, 0.0000756283, 0.0000708033, 0.000066779, 0.0000636471, 0.0000625116,0.0000665943, 0.000074074, 0.0000774592, 0.0000738344, 0.0000684751, 0.0000655744, 0.0000637559, 0.0000632316, 0.0000675249, 0.0000746401, 0.0000765622, 0.0000713567, 0.0000660968, 0.0000648676, 0.0000644101, 0.000064073, 0.0000680156,0.0000743922, 0.0000748728, 0.0000685322, 0.0000639731, 0.0000647345, 0.0000654567, 0.0000648017, 0.0000679187, 0.0000733889, 0.0000726689, 0.0000657091, 0.0000622946, 0.0000651115, 0.0000666921, 0.0000652615, 0.0000672442, 0.0000718318, 0.0000702735, 0.0000631592, 0.0000611172, 0.0000658463, 0.0000679338, 0.0000654099, 0.0000661311, 0.0000699868, 0.0000679712, 0.0000610429, 0.0000603915, 0.0000667595, 0.0000690611, 0.0000653029, 0.0000647858, 0.0000681115, 0.0000659659, 0.0000594197, 0.0000600132, 0.0000676898, 0.0000700163, 0.0000650527, 0.000063423, 0.0000664129,0.0000643775, 0.0000582827, 0.0000598674, 0.0000685134, 0.000070784, 0.0000647821, 0.0000622261, 0.0000650355, 0.0000632614,0.0000575952, 0.000059858, 0.0000691461, 0.0000713679, 0.0000645938, 0.0000613302, 0.000064069, 0.0000626336, 0.0000573173,0.0000599219, 0.0000695408, 0.0000717756, 0.0000645558, 0.0000608195, 0.0000635588, 0.0000624885, 0.0000574204, 0.0000600333, 0.0000696834, 0.0000720124, 0.0000646977, 0.0000607281, 0.0000635126, 0.0000628061, 0.0000578888, 0.0000602007, 0.0000695902, 0.0000720824, 0.0000650125, 0.0000610423, 0.0000639015, 0.0000635503, 0.0000587147, 0.0000604608, 0.0000693062, 0.0000719916, 0.000065463, 0.0000617039,0.0000646594, 0.000064664, 0.0000598881, 0.0000608677, 0.0000689002, 0.0000717529, 0.0000659909, 0.0000626183, 0.0000656854, 0.0000660624, 0.0000613839, 0.0000614786, 0.0000684577, 0.0000713905, 0.0000665298, 0.0000636677, 0.0000668497, 0.0000676302, 0.0000631474, 0.000062335, 0.0000680682,0.0000709408, 0.0000670184, 0.0000647289, 0.0000680081, 0.0000692241, 0.0000650845, 0.0000634439, 0.0000678097, 0.0000704504, 0.0000674126, 0.000065693, 0.0000690214, 0.0000706853,0.00006706, 0.000064764, 0.0000677327, 0.0000699684, 0.0000676912, 0.000066482, 0.0000697781, 0.0000718607, 0.0000689098, 0.0000662045,0.0000678498, 0.0000695389, 0.0000678562, 0.0000670585, 0.0000702138, 0.000072631, 0.0000704663, 0.0000676364, 0.0000681344,0.0000691935, 0.0000679274, 0.0000674255, 0.0000703228, 0.0000729367, 0.0000715913, 0.0000689162, 0.0000685272, 0.0000689492, 0.0000679364, 0.0000676184, 0.0000701554, 0.000072794,0.0000722085, 0.0000699157, 0.0000689494, 0.0000688079, 0.0000679212, 0.0000676936, 0.0000698037, 0.0000722933, 0.0000723258, 0.0000705539, 0.0000693212, 0.0000687577, 0.00006792, 0.0000677163, 0.0000693786, 0.0000715782, 0.0000720359, 0.0000708189, 0.0000695815, 0.0000687748, 0.000067962, 0.0000677458,0.0000689833, 0.0000708076, 0.0000714897, 0.0000707694, 0.0000697032, 0.0000688285, 0.0000680579, 0.0000678211, 0.0000686895, 0.0000701136, 0.0000708499, 0.00007051, 0.0000696956, 0.0000688882, 0.000068197, 0.000067952, 0.0000685249, 0.0000695739, 0.0000702467, 0.0000701544, 0.0000695939, 0.0000689322, 0.0000683544, 0.000068123, 0.0000684773, 0.0000692078, 0.0000697549,0.0000697941, 0.0000694432, 0.0000689511, 0.0000685038, 0.0000683059, 0.000068511, 0.0000689924, 0.0000693973, 0.0000694848,0.0000692835, 0.0000689472, 0.000068627, 0.0000684739, 0.0000685852, 0.0000688856, 0.0000691611, 0.0000692488, 0.0000691419, 0.0000689291, 0.0000687172, 0.0000686102, 0.0000686674, 0.0000688449, 0.0000690179, 0.0000690851, 0.0000690317, 0.0000689062, 0.0000687771, 0.0000687096, 0.0000687381, 0.0000688373, 0.0000689375, 0.0000689807, 0.0000689548, 0.0000688857, 0.0000688133, 0.0000687752, 0.0000687896, 0.0000688418, 0.0000688953, 0.0000689191, 0.0000689065, 0.0000688709, 0.0000688339, 0.0000688149, 0.0000688224, 0.0000688483, 0.0000688742, 0.0000688855, 0.0000688791, 0.000068862, 0.0000688449, 0.0000688367, 0.0000688408,0.0000688527, 0.0000688641, 0.0000688686, 0.0000688653, 0.0000688577, 0.0000688507, 0.0000688478, 0.0000688499, 0.000068855,0.0000688594, 0.0000688608, 0.0000688591, 0.0000688561, 0.0000688535, 0.0000688527, 0.0000688538, 0.0000688558, 0.0000688573, 0.0000688576, 0.0000688568, 0.0000688558, 0.000068855,0.0000688549, 0.0000688554, 0.000068856, 0.0000688564, 0.0000688564, 0.0000688561, 0.0000688557, 0.0000688556, 0.0000688556, 0.0000688558, 0.000068856, 0.0000688561, 0.0000688561,0.000068856, 0.0000688559, 0.0000688559, 0.0000688559, 0.0000688559, 0.000068856, 0.000068856};

cwd=ContinuousWaveletTransform[data2, GaborWavelet[6], {Automatic, 12}]
WaveletScalogram[cwd, ColorFunction -> "RustTones"]

enter image description here

Spectrogram[data2, ColorFunction -> "RustTones"]

enter image description here

Just a critique - ContinuousWaveletTransform uses a SampleRate -> 8000 whereas you are using SampleRate -> 1023 as an option in the Spectrogram. — Sektor, Oct 21 '13 at 20:19
@NikolaDimitrov I thought SampleRate would only effect the axes labels, since it is just an overall factor. Not true? — xslittlegrass, Oct 21 '13 at 20:23
Yes, in this case I think it affects only the axis, so you are right :) — Sektor, Oct 21 '13 at 20:29

score 8 · Accepted Answer · answered Oct 21 '13 at 19:59

8

The Spectrogram function also allows you to alter the window length, overlap and apply a windowing function to your data segment before FFT. You'll get better results if you utilize those (which requires some knowledge of DSP and your specific problem) instead of using the default parameters and the rectangle window.

For instance, the following shows the frequencies distinctly:

Spectrogram[data, 128, 64, BlackmanWindow, SampleRate -> 1023, 
    FrameLabel -> {"Frequency(Hz)", "Time"}]

answered Oct 21 '13 at 19:59

rm -rf

88,781
21
293
472

Khhhhhhh... Got home late .. :D Nuttin +1 :) – Sektor Oct 21 '13 at 20:08
Thanks for the answer. I added a second example, could you also give me some hint and explanation on how to choose these parameters for the second one as well? I actually played with the second, third and forth parameters for a while (for both examples) before I posting the question here, and I couldn't find any combinations that give me a clear plot. – xslittlegrass Oct 21 '13 at 20:32
@xsl What is the sampling rate for data2? There aren't any magic parameters... just playing with the numbers and getting a "pretty plot" is not the way to do it – you might end up with absolute rubbish results, but nevertheless a nice plot. What you really need is a crash-course in DSP, and it's more than I can cover in an answer here. You can try reading through these articles — TF analysis, Windows, Spectrogram and the linked articles. – rm -rf Oct 21 '13 at 20:57
@rm-rf A collaboration on an article/s about DSP :D ? – Sektor Oct 21 '13 at 21:16
@rm-rf The sampling rate for data2 is the same 1023. I though the sampling rate only give an overall factor and not effect the results, right? Thanks for providing these links. – xslittlegrass Oct 21 '13 at 21:25
@xslittlegrass It's just a matter of dynamic scaling. The information is there, but your choice of color function is making it hard to see. Try using SpectrogramArray to get the data and plot it in a logarithmic scale. A simple example: sp = SpectrogramArray[data2, 128, 64, BlackmanWindow]; ListDensityPlot[Transpose@Abs[sp[[;; , ;; 64]]]^2 // Log10, AspectRatio -> 1, ColorFunction -> ColorData[{"SunsetColors", "Reversed"}]] I'll leave the ticks and stuff to you. – rm -rf Oct 21 '13 at 21:35
1

@NikolaDimitrov There's an entire site for DSP: [dsp.se] :D – rm -rf Oct 21 '13 at 21:36
1

@rm-rf I know, but we are better :D :D – Sektor Oct 21 '13 at 21:37

score 3 · Answer 2 · answered May 22 '14 at 05:39

Actually, we can get linear scale rather than log scale using wavelet transform, using the "LinearScalogramFunction" property of a ContinuousWaveletData object.

This is the default wavelet scalogram:

sampleRate = 1023;
data = Table[
   Piecewise[{{Sin[2 π 10 t], 0 <= t < 1/4}, {Sin[2 π 25 t], 
      1/4 <= t < 1/2}, {Sin[2 π 50 t], 
      1/2 <= t < 3/4}, {Sin[2 π 100 t], 3/4 <= t <= 1}}], {t, 0, 
    1, 1/sampleRate}];
cwd = ContinuousWaveletTransform[data, 
   DGaussianWavelet[5], {Automatic, 12}, SampleRate -> sampleRate];
WaveletScalogram[cwd, ColorFunction -> "RustTones"]

enter image description here

This uses the "LinearScalogramFunction" property to get a linear function and then plot the linear scale function using DensityPlot

f = cwd["LinearScalogramFunction"];
scaleToFrequency[
   s_] = (cwd["SampleRate"]/(s*cwd["Wavelet"]["FourierFactor"]));
DensityPlot[Abs[f[x, scaleToFrequency[y]]], {x, 0, 1}, {y, 2, 100}, 
 PlotPoints -> {300, 100}, ColorFunction -> "RustTones", 
 ClippingStyle -> Automatic, 
 FrameLabel -> {"Time (second)", "Frequency (Hz)"}]

enter image description here

score 2 · Answer 3 · answered Oct 21 '13 at 21:29

2

Urghhh ... I hate those "RustTones"... Nevertheless ^o^

sa = SpectrogramArray[data2];
ListDensityPlot[Transpose@Abs@sa, ColorFunction -> "DeepSeaColors", 
                AspectRatio -> 1/2, Frame -> None]

ListDensityPlot[Transpose@Abs@sa, ColorFunction -> Hue, 
                AspectRatio -> 1/2, Frame -> None]

answered Oct 21 '13 at 21:29

Sektor

3,320
7
27
36

Does that provide enough information ? – Sektor Oct 21 '13 at 21:30
1

That's great, thanks a lot! – xslittlegrass Oct 21 '13 at 21:56

How to increase Spectrogram resolution?

3 Answers3

Linked