To get what was said in the comments on record as an answer.
Chop is probably what you are looking for.
expr =
a (0.25 + 0. b) + b^2 (0. + 0./c) + b (-1. + 0. c) - 0.5 c +
(b (-1. b - 0.5 c) c)/a^2 // Chop
0.25 a - 1. b - 0.5 c + (b (-1. b - 0.5 c) c)/a^2
You might want to go further
expr = expr /. {1. x_ :> x, -1. x_ :> -x}
0.25 a - b - 0.5 c + (b (- b - 0.5 c) c)/a^2
Update
In general expressions with inexact coefficients can contain the forms 0.x, 1.x, and -1.x. None of these cause computation difficulties, but they are unattractive, and often we want to eliminate them.
With a help from Mr.Wizard, I offer the following pattern to do this task.
fixerPattern = u_ /; Sign[u] == u :> Sign[u]
With this we can clean up
expr =
a (0.25 + 0. b) + b^2 (0. + 0./c) + 1.b (-1. + 0. c) - 0.5 c +
(b (-1. b - 0.5 c) c)/a^2
without using Chop and it takes care of the instances of both 1.b and -1.b.
expr /. fixerPattern
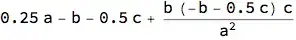
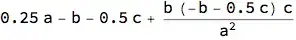
expr /. {x_Real /; x==0 -> 0}– ssch Oct 28 '13 at 17:32SetOptions[Simplify, TransformationFunctions :> Function[x, x //. {0. -> 0, 1. y_ :> y, -1. y_ :> y}]]and thenSimplifysimplifies as you want. – Rolf Mertig Oct 28 '13 at 18:29-1. y_ :> -y– RunnyKine Oct 28 '13 at 20:15