5

I am trying to get plot for the band structure for graphene.

d = 10; (*Plot range*) 
coupling := {{0, 2 Cos[Sqrt[3]*(#1)/2]*Cos[#2/2] + Cos[#2] + 
I (2 Cos[Sqrt[3]*(#1)/2]*Sin[#2/2] - Sin[#2])}, 
{Conjugate[ 2 Cos[Sqrt[3]*(#1)/2]*Cos[#2/2] + Cos[#2] + 
   I (2 Cos[Sqrt[3]*(#1)/2]*Sin[#2/2] - Sin[#2])], 0}} &;
Plot3D[Eigenvalues[coupling[kx, ky]][[1]], {kx, -d, d}, {ky, -d, d}] (*Discontinuous*)
Plot3D[(Eigenvalues[coupling[kx, ky]][[1]])^2, {kx, -d, d}, {ky, -d, d}] (*Continuous*)

I am not able to understand why the surface in the first plot is coming out discontinuous; i.e., it has some gaps in the surface plot, whereas there are no gaps in the second plot, which simply plots the square of the function shown in the first plot.

There is no physics that explains the gaps. Also, the effect is not periodic/predictable. By that I mean that on changing d, I am getting very different patterns of gaps all over the place.

Is there some problem with my code or is 3D plot working incorrectly? How do I get rid of this error?

Edit

I am NOT talking about the spike at (0,0). I am attaching a picture of my plot for clarity. I am talking about the "ribbons" missing from the surface.

enter image description here

There are no "ribbons" in the case of the squared plot.

enter image description here

Community
  • 1
typesanitizer
  • 374
  • 1
  • 11
  • 3
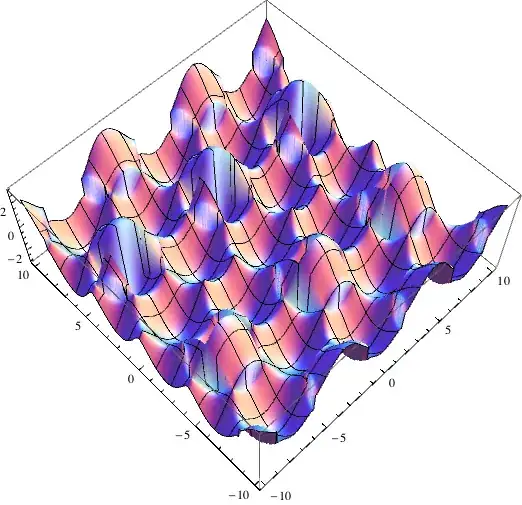
    It's the spike at $(0,0).$ Try adding Exclusions->{{0,0}} as an option to the discontinuous plot. – gpap Oct 30 '13 at 10:53
  • That is not the issue for me. I hope the question is clearer after the EDIT. – typesanitizer Oct 30 '13 at 12:40
  • 1
    With Exclusions->{{0,0}} I don't get any missing ribbons, can you clarify how it doesn't work? – ssch Oct 30 '13 at 12:54
  • The Exclusions->{{0,0}} method works for me, although I am not sure why. @MichaelE2 , I am not sure how your explanation accounts for the fact that the "ribbons" are missing in the squared plot without accounting for the branch-switch explicitly. – typesanitizer Oct 30 '13 at 13:41
  • This shows that the branch switches are consistent across plot scales: 'Module[{cp}, cp[d_] := ContourPlot[ First[Eigenvalues[coupling[kx, ky]]], {kx, -d, d}, {ky, -d, d}, ImageSize -> 300]; Grid[{cp /@ {5, 10, 15}}] ]' – Daniel Flatin Oct 30 '13 at 14:11
  • I posted the comment under the assumption that the adaptive sampling of plotpoints was to blame for the ribbons i.e. the plotting of the spike required many plot points. But with MaxRecursion->0 the problem remains. I think @MichaelE2 is right as per its cause and excluding $ (0,0) $ probably fixes it by forcing numerical evaluation rather than changing the sampling. – gpap Oct 30 '13 at 14:45
  • @gpap if the exclusion is forcing it to use numerical evaluation, why am I not getting similar ribbons in the squared plot without using Exclusion->{{0,0}}? – typesanitizer Oct 30 '13 at 17:13
  • Could be the automatic Exclusion setting that detects discontinuities where there aren't any, Exclusions->None has no ribbons. – ssch Nov 02 '13 at 22:51

1 Answers1

3

This is just to get the answer given in the comments on record.

The solution to the ragged plot problem is to make two changes to the the OP's code

  1. Define a function

    eigen[kx_?NumericQ, ky_?NumericQ] = Evaluate @ Eigenvalues[coupling[kx, ky]][[1]];

  2. Plot the function eignen[kx, ky] with the options PlotPoints -> 100, Exclusions -> {{0, 0}}.

    Plot3D[eigen[kx, ky], {kx, -d, d}, {ky, -d, d}, 
  PlotPoints -> 100, Exclusions -> {{0, 0}}]

3DPlot.png

m_goldberg
  • 107,779
  • 16
  • 103
  • 257