7

This question is originally part of this question, but this issue seems to be different from the former one, so I think it's better to start another question for it.

Usually, human can't hear sound with a frequency lower than 20 Hz, but what's confused is, the output of the following code can generate very slight shrieks, to be precise, two shrieks for every period, and the pitch of the sound will be lower with lower SampleRate:

Play[Sin[2 Pi t], {t, 0, 1}]
Play[Sin[2 Pi t], {t, 0, 1}, SampleRate -> 4000]
Play[Sin[2 Pi t], {t, 0, 1}, SampleRate -> 2000]

After some trial, I noticed that the frequency of the slight shrieks seems to be equal to the SampleRate, i.e.

  Play[Sin[2 Pi t], {t, 0, 5}, SampleRate -> 2000]

and

  Play[Sin[2000 2 Pi t], {t, 0, 1}, SampleRate -> 4000 2 Pi]

have same pitch. (Remember to regulate volume since the shriek generated by the former sample is really slight. )

It's probably another kind of artifact, but can someone explain it in detail?

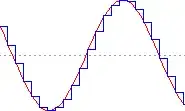
Some more information: the shrieks are at the position of peaks and valleys of sine wave i.e.

Play[Sin[2 Pi t], {t, 0, 1}, SampleRate -> 2000]

has $2$ shrieks while

Play[Cos[2 Pi t], {t, 0, 1}, SampleRate -> 2000]

has $0.5+1+0.5$ shrieks.

Edit:

I should admit that I've misheard the position of the shrieks. With the code below, it's easy to distinguish that there's no sound at peaks and valleys:

Column[{Animate[Plot[Sin[2 Pi u], {u, 0, t}, PlotRange -> {{0, 5}, {-1, 1}}], 
                {t, 0, 5}, AnimationRate -> 1, AnimationRepetitions -> 1], 
        EmitSound@Play[Sin[2 Pi t], {t, 0, 5}, SampleRate -> 2000]}]

I've posted the question in sound.SE and the answer I got there is in line with @CL.'s answer. Click here to read the answer (with a self-made video!).

Community
  • 1
xzczd
  • 65,995
  • 9
  • 163
  • 468

2 Answers2

20

When you use a very low sample rate, the signal is represented with very few samples. If you are using a very stupid resampler that creates 48 kHz data by just repeating samples, you get a wave form like the blue one below:
sine wave
A better resampler would create the red wave form.

Now, the difference between these two wave forms looks like this:
quantization noise
This is approximately a saw tooth wave at a frequency of the original low sample rate (2 or 4 kHz).

A human ear does not detect waveforms, it detectes frequencies.
So when you play back the blue wave form, the sound in your ear is a combination of two frequencies, the original low-frequency sine wave, and the sawtooth noise. The original low-frequency sine wave has a frequency too low to be actually heard, so you hear only the noise.

Also see quantization noise on Wikipedia.

CL.
  • 481
  • 5
  • 8
  • 3
    If this is indeed the cause then the effect should be considerably stronger with SampleDepth -> 8. This provides a means of testing if this is the real cause. – Szabolcs Nov 07 '13 at 17:53
  • 5
    Not only can the human ear not detect a 1 Hz tone, I would be very surprised if your laptop speaker could reproduce a 1 Hz tone. Laptop speakers are tiny little things and are way smaller than a 1 Hz wavelength of 343 meters. The only you could possibly be hearing under a continuous sine wave would be the very high distortion products of the speaker and the amplifier. Since you are probably not driving the speaker that hard, I would have to vote for the sampling noise as being the source. (Source: I am an electroacoustics engineer.) – Daniel W Nov 07 '13 at 18:54
  • 1
    @DanielW I would love 343 meter loudspeakers. Think of those bass lines! – cormullion Nov 07 '13 at 22:26
  • @DanielW: I'm curious, what's the connection between speaker size and sound wavelength? For example, I can produce a 50Hz signal with my speakers, although they're much smaller than the 6.9m wavelength. – Niki Estner Nov 08 '13 at 14:43
  • 1
    @nikie There isn't mich of a connection; sound is a longitudinal wave. Larger speakers are used for low tones because it would require an insanely strong magnetic field to make a small membrane vibrate at a low frequency. (The same applies to large membranes and high frequencies.) – CL. Nov 08 '13 at 17:06
  • 2
    @nikie A first-year physics, first-order approximation is that at fixed intensity, the amplitude and frequency are inversely proportional, and the max. acceleration is proportional to frequency. It's much easier for a larger speaker to have a larger amplitude for low frequencies. But a larger cone is more massive and harder to accelerate at high frequencies. Acoustics is probably more complicated than that, beyond my understanding, and I'll let the experts estimate the error term of this comment. – Michael E2 Nov 09 '13 at 13:42
  • 1
    @nikie (just my humble guess) what Michael said makes sense to me. Also, with a larger speaker you don't need as much intensity for some power output (more area). So the area makes up for the need of higher particle displacement, while at the same time making it easier to resonate low (higher mass). But if power isn't an issue, even speakers as tiny as earplugs can have good enough lows if you put them inside your ears, right? – Rojo Nov 11 '13 at 06:30
  • @Rojo: Yes, it makes sense to me, too, now. You learn something new every day. – Niki Estner Nov 11 '13 at 08:40
4

How well a speaker can radiate sound is related to its radiation impedance, the red curve here. When a speaker is very small compared to the wavelength, $k a\ll 1$, so its radiation impedance is extremely low. The cone might be moving, but it just is not able to produce sound with that motion very effectively.

This is not true of sealed insert earphones or hearing aids. They produce sound by compressing the small volume of air trapped in the ear canal, so the sound pressure $p\propto \Delta V/V$. The smaller the ear canal volume $V$, the louder the sound for the same diaphragm motion. This is why you can get good low frequency response from such a small device, as long as your ear-domes are well sealed to your canal walls.

Daniel W
  • 3,416
  • 18
  • 31